Вывод формул численного дифференцирования

АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ

Посредством дифференцирования интерполяционных фор­мул выводятся формулы для приближенного вычисления произ­водных. Остаточные члены полученных приближенных формул находятся с помощью формулы Тейлора и дифференцированием соответствующих остаточных членов интерполяционных фор­мул. Особая роль придается простейшим аппроксимациям перво­го и второго порядков точности первой и второй производных в узлах сетки, что существенно используется в последующих гла­вах. Обращается внимание на существование таких шагов аппроксимации производных по формулам различных порядков точности, при которых ограниченная точность вычисленных значений функции наименьшим образом влияет на точность результата.

Численное дифференцирование, т.е. нахождение значений производных заданной функции f(x) в заданных точках х, в от­личие от рассмотренного в предыдущей главе численного интег­рирования, можно считать не столь актуальной задачей в связи с отсутствием принципиальных трудностей с аналитическим нахож­дением производных. Однако имеется ряд моментов, не позво­ляющих обходить эту задачу стороной. Это и типичное для при­кладных задач незнание аналитического вида f(x), и возможное сильное усложнение функции при ее аналитическом дифференци­ровании (что затрудняет нахождение ее значений с высокой точ­ностью), и желательность получения значений производных с по­мощью однотипных вычислительных процессов без привлечения аналитических выкладок. Главным же для дальнейшего является потребность в простых формулах, с помощью которых производ­ные в заданных точках можно аппроксимировать несколькими значениями функции (быть может, неизвестной) в этих и близких к ним точках.

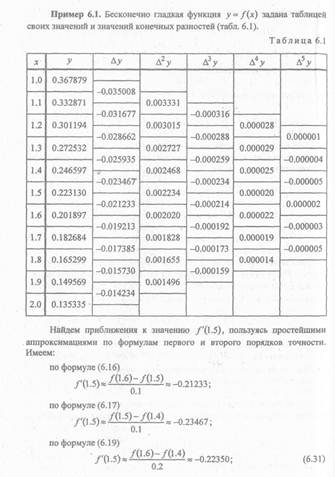
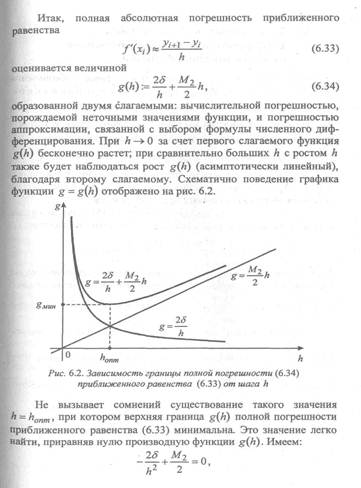
Дата добавления: 2014-01-20