Это норма разности векторов

Введем еще одно важное определение, скалярное произведение, это

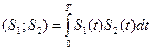. (3)

Если скалярное произведение равно нулю, такие сигналы называются ортогональными.

Найдем его для наших гармонических сигналов:

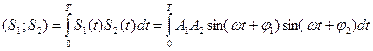
. Представив произведение тригонометрических функции как sin(x)sin(y)=1/2cos(x-y)-1/2cos(x+y), получим два интеграла. Первый

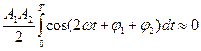, функция косинуса знакопеременная (интеграл это площадь).

Второй

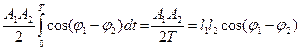. (4)

Это скалярное произведение гармонических сигналов,

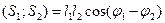, (5)

и оно входит в норму разности (2).

Что же следует из векторного представления? Вывод таков. Чем дальше друг от друга концы векторов, тем достовернее можно различить сигнал на фоне помех (см. рис. 6). «Развести»концы векторов можно увеличением норму вектора сигнала, иными словами увеличить мощность передатчика, и увеличением нормы разности d, то - есть уменьшить скалярное произведение. Это возможно определенным выбором сигналов. В нашем примере с гармоническими сигналами этому соответствуют сигналы с противоположной фазой, φ₁-φ₂=π.

Существует несколько видов пространств для представления многомерных сигналов.

Линейное пространство. Обладает следующими свойствами.

Определены расстояния между векторами d. Если вектора равны, d=0.

При сложении векторов складываются их координаты.

Норма вектора ‌‌‌‌║x║=√x_i², где x_i –координаты вектора.

Норма разности ║x-y║=√∑(x_i-y_i)².

Скалярное произведение (x;y)=║x║║y║cosφ.

Скалярное произведение ортогональных сигналов равно нулю.

N – мерное Евклидово пространство имеет конечное число координат. Если N=∞, такое пространство называется Гильбертовым.

Случайность принимаемых сигналов заставляет привлечь к анализу статистические законы. Это W(y/S_i) – условный закон распределения плотности вероятности принимаемого сигнала при условии передачи Si-го сигнала или более кратко - функция правдоподобия. Это первая статистическая характеристика в задаче приема. Помимо этого вводятся априорные (доопытные) вероятности сигналов p(Si).

Как и прежде, будем считать, что множество точек в пространстве образуют пространство принимаемого сигнала Y. Принимая сигналы y(t) приемник должен решить, какой сигнал был передан. Для этого всё Y необходимо поделить на области. В нашем примере это β₀ и β₁. Если у(t) попал в область β₀, то следует выносить решение в пользу S_0, если в β₁- S₁. Очевидно, что вероятность правильного приема р_пр определятся совпадением двух событий: передачи конкретного сигнала и его попадания в нужную область. поэтому

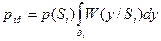, (6)

а вероятность ошибки

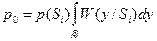, (7)

при i≠j.

При множестве сигналов будем иметь множество областей β_i (рис. 8).

Y – пространство принимаемого сигнала

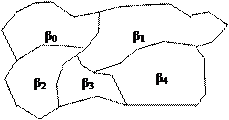
Рис. 8 Области сигналов в пространстве Y.

Возникает вопрос, как назначать эти области? Здесь имеется некоторая неоднозначность. При увеличении одной из них, b_i, увеличивается вероятность правильного приема данного сигнала, но одновременно с этим уменьшаются эти же вероятности для других, соседних, сигналов. К тому же растут вероятности ошибочного попадания в эту область. Из этого следует вывод о том, что области в пространстве должны быть выбраны по определенным правилам, которые называются критериями оптимального приема. В их основе отражается одна из задач приема: обнаружение сигнала, различение сигнала, восстановление сигнала. Первые две применяются в дискретных каналах связи, последняя, в основном, в аналоговых системах.

Критерий минимального среднего риска.

В нем ставится задача различения сигнала. Введем функцию потерь J(λ,λ′), где λ – переданное сообщение, λ′ - принятое сообщение (оценка). Эта функция является случайной и обладает следующим очевидным свойством: J(λ,λ′)=0 при l=l` и J(λ,λ′)¹0 при l¹l`. Введем W(λ,λ′) – двумерную плотность распределения переданного и принятого сообщений.

По обычным формулам статистики найдем среднее значение функции потерь, это и будет средний риск средний риск:

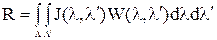. (8)

При регулярном правиле решения принятому сигналу y(t) жестко соответствует вынесенная оценка

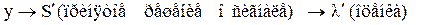, поэтому в статистиках аргумент l` может быть заменен принятым сигналом y. И тогда средний риск будет

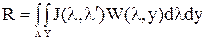. (9)

Воспользуемся формулой Байеса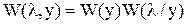и тогда

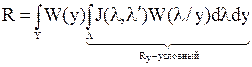. (10)

Внутренний интеграл получил название условного среднего риска.

Дата добавления: 2014-01-20