Расчет и прогнозирование норм показателей надежности

На стадии разработки используется расчетный метод оценки показателей надежности. В этот период может использоваться также, и расчетно-экспериментальный метод, если известны результаты испытаний на надежность по составным частям изделия.

Расчетный метод применяется в том случае, когда известны табличные значения интенсивности отказов элементов l_i. В этом случае используется экспоненциальный закон времени возникновения внезапных отказов. Зная величину l_i можно определить вероятность безотказной работы P_i(t) и среднее время безотказной работы (наработку до отказа) Т_СР каждого i-го элемента по формулам:

P_i(t_З)=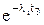 и Т_срi=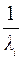, (2.11)

где t_З - заданное время боевого применения – t_БП, или подготовки - t_ПОД, или ожидания – t_ОЖ.

Рассчитав по формуле (2.11) значения P_i(t_З) для всех i-х элементов системы (блока, устройства) и составив структурную схему расчета надежности системы, можно определить вероятность безотказной работы системы – P_C(t_З) и наработку до отказа – Т_ср.

Для прогнозирования показателей долговечности (_Рi, Т_Рg, _СЛ, Т_СЛg) и сохраняемости (_С, Т_Сg) можно использовать известные коэффициенты вариации V, которые определяются по формуле

V_t=, (2.12)

где 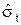=S_t - оценка среднего квадратического отклонения, определяемая по формуле:

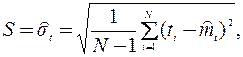(2.13)

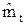- оценка математического ожидания, определяемая по формуле:

, (2.14)

t_i - значения показателей долговечности и сохраняемости изделий-прототипов.

Зная величины 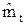и V, можно определить гамма-процентные показатели долговечности и сохраняемости для нормального закона по формуле:

T_ig=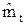-z_g×S_t=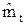-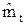×V_t×z_g=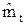(1- V_t×z_g). (2.15)

где z_g - квантиль нормального закона определяется из таблиц по заданной величине g.

По известной величине коэффициента вариации можно определить и показатель закона распределения Вейбулла. В этом случае можно прогнозировать показатели долговечности и сохраняемости, подчиняющиеся закону распределения Вейбулла.

Для большинства элементов механических систем табличные интенсивности отказов отсутствуют.

В этом случае используют расчетно-экспериментальный метод прогнозирования показателей надежности по прототипам. Для этого обычно составляются регрессионные модели. Покажем применение этого метода на примере.

Пример. Определить зависимость показателя ОТП (коэффициента готовности К_Г) в режиме ожидания – К_Г(t_ОЖ) для образца от трех факторов: Х₁ - начальная скорость V₀ м/с, Х₂ - масса q, кг, Х₃ - диаметр - d(мм).

Для решения этой задачи используем 10 образцов-прототипов (ближайших аналогов проектируемого образца). Используем метод построения статистической модели для пассивного эксперимента. Исходные данные по прототипам приведены в табл. 2.6.

Таблица 2.6

Исходные данные

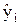
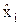
Характеристика	Обозначения	Значения характеристик 10 образцов		S^2i
КГ	у	0,93	0,87	0,84	0,80	0,86	0,8	0,78	0,86	0,8	0,65	0,82	0,07
V0 м/с	Х1
q, кг	Х2	1,6	9,4	21,8	25,0	21,8	33,4	43,6		43,6		33,4	27,3
d, мм	Х3												39,9

Данная задача решается по программе «Линейная многофакторная модель» на ЭВМ.

В результате решения получим.

1. Значения коэффициентов модели:

b₀=1,07; b₁= -0,7×10^-4; b₂= -0,12×10^-2; b₃= -0,13×10^-2.

2. Опытное (расчетное) значение критерия Фишера -F_РАС= 4,1.

После этого составляем регрессивную модель

у=К_Г(t_ОЖ)=1,07-0,7×10^-4×Х₁ -0,12×10^-2×Х₂ -0,13×10^-2×Х₃. (2.16)

Далее проверяем модель (2.16) на адекватность по критерию Фишера:

F_РАС=4,1<7,98=F_ТАБЛ(a=0,1; f₁=N-1=9; f₂=N-(к+1)=6),

где N - количество прототипов, к – количество факторов.

Следовательно, модель линейна и адекватна и ее можно использовать для прогнозирования К_Г(t_ОЖ) проектируемых образцов на стадии разработки. Для этого необходимо подставить в модель (2.16) факторы Х₁, Х₂, Х₃ проектируемого образца.

В дальнейшем, при испытаниях, когда будут получены исходные данные по опытному образцу, значение К_Г(t_ОЖ) будет рассчитано и уточнено.

Приведенный расчетно-экспериментальный метод прогнозирования показателей надежности на основе пассивного эксперимента может применяться для любых показателей надежности.

Дата добавления: 2014-01-20