Понятие о двухфакторном дисперсионном анализе

Предположим, что в рассматриваемой в п. 1.1 задаче о качестве различных (т)партий изделия изготавливались на разных (l)станках и требуется выяснить, имеются ли существенные различия в качестве изделий по каждому фактору: А – партия изделий, В – станок. В результате мы приходим к задаче двухфакторного дисперсионного анализа.

Все имеющиеся данные представим в виде таблицы, в которой по строкам – уровни A_i фактора А, по столбцам – уровни B_j фактора В, а в соответствующих клетках, или ячейках, таблицы находятся значения показателя качества изделий x_ijk (i =1,2,…, m; j =1,2,…, l; k =1,2,…, n):

B A	B1	B2	…	Bj	…	Bl
A1 A2 … Ai … Am	x111,…,x11 k x211,…,x21 k … x i 11,…,x i 1 k … x m 11,…,x m 1 k	x121,…,x12 k x221,…,x22 k … x i 21,…,x i 2 k … x m 21,…,x m 2 k	… … … … … …	x1 j 1,…,x1 jk x2 j 1,…,x2 jk … x ij 1,…,x ijk … x mj 1,…,x mjk	… … … … … …	x1 l 1,…,x1 lk x2 l 1,…,x2 lk … x il 1,…,x ilk … x ml 1,…,x mlk

Групповые средние находим по формулам:

в ячейке – 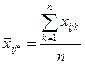(6)

по строке – (7)

по столбцу – 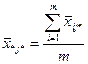(8)

Общая средняя: 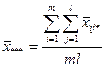(9)

Таблица дисперсионного анализа имеет вид:

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средний квадрат
Межгрупповая (фактор А)		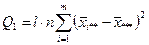m – 1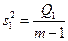
Внутригрупповая (фактор В)		l – 1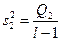
Взаимодействие (АВ)		(m – 1)(l – 1)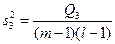
Остаточная		m·l·n – m·l
Общая		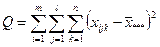m·l·n – 1

Проверка нулевых гипотез Н_А, Н_В, Н_АВ об отсутствии влияния на рассматриваемую переменную факторов А, В и их взаимодействия АВ осуществляется сравнением отношений 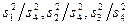(для модели I с фиксированными уровнями факторов) или отношений (для случайной модели II) с соответствующими табличными значениями F -критерия Фишера-Снедекора. Для смешанной модели III проверка гипотез относительно факторов с фиксированными уровнями проводится так, как в модели II, а факторов со случайными уровнями – как в модели I.

Если n =1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены, так как выпадает компонента Q₃ из общей суммы квадратов отклонений, а с ней и средний квадрат 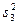, ибо в этом случае не может быть речи о взаимодействии факторов.

Задача 1.

В двухфакторном комплексе приводится сменная выработка рабочего в зависимости от типа станка (А) и стажа его работы (В). При α=0.01 проверить влияние факторов А и В на сменную выработку рабочего (таблица Б1):

	А1	А2	А3
Вариант 1
В1
В2
В3

Дата добавления: 2014-01-20