Смачивание

Из практики известно, что капля воды растекается на чисто вымытом стекле и принимает форму, изображённую на рисунке 17.7.

Рис. 17.7. Форма поверхности капли при смачивании поверхности твёрдого тела жидкостью. (Рис. 98 из Трофимовой, стр. 131).

В то же время ртуть, помещённая на такое же чисто вымытое стекло, превращается в сплюснутую каплю (см. рисунок 17.8).

В первом случае говорят, что жидкость смачивает поверхность твёрдого тела, а во втором – не смачивает её.

Рис. 17.8. Форма поверхности капли при несмачивании поверхности твёрдого тела жидкостью. (Рис. 98 из Трофимовой, стр. 131).

Для жидкости, смачивающей поверхность твёрдого тела, силы притяжения между молекулами жидкости и твёрдого тела больше, чем между молекулами самой жидкости, и жидкость стремится увеличить поверхность соприкосновения с твёрдым телом (жидкость " растекается " по поверхности твёрдого тела).

Для несмачивающей жидкости силы притяжения между молекулами жидкости и твёрдого тела меньше, чем между молекулами жидкости, и жидкость стремится уменьшить площадь поверхности соприкосновения с твёрдым телом.

Рассмотрим подробнее рисунки 17.7 и 17.8. К линии соприкосновения трёх сред (жидкость, твёрдое тело и, например, воздух) приложены три силы поверхностного натяжения, которые направлены по касательной внутрь поверхности соприкосновения соответствующих двух сред (на рисунках 17.7 и 17.8 точка О есть пересечение линии соприкосновения трёх сред с плоскостью чертежа).

Эти силы, отнесённые к единице длины линии соприкосновения, равны соответствующим поверхностным натяжениям σ₁₂ , σ₁₃ , σ₂₃ . Угол θ между касательными к поверхности жидкости и поверхности твёрдого тела называется краевым углом. Условием равновесия капли, изображённой на рисунке 17.7, является равенство нулю суммы проекций сил поверхностного натяжения на направление касательной к поверхности твёрдого тела, т.е.:

, (17.18)

откуда следует условие:

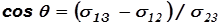, (17.19)

Из условия (17.19) следует, что краевой угол θ может быть острым или тупым, в зависимости от значений величин σ₁₃ и σ₁₂.

Если σ₁₃ > σ₁₂, то cos θ > 0 и угол θ – острый (см. рис. 17.7), т.е. жидкость смачивает поверхность твёрдого тела. Если σ₁₃ < σ₁₂, то cos θ < 0 и угол θ – тупой (см. рис. 17.8), т.е. жидкость не смачивает поверхность твёрдого тела.

Если выполняется условие σ₁₃ > σ₁₂ + σ₂₃, то жидкость растекается по поверхности твёрдого тела, покрывая его тонкой плёнкой (керосин по металлу) – в этом случае говорят, что имеет место полное смачивание (θ = 0). Если же выполняется условие σ₁₂ > σ₁₃ + σ₂₃, то жидкость будет стягиваться в шарообразную каплю, имея с поверхностью твёрдого тела в пределе только одну точку соприкосновения - в этом случае говорят, что имеет место полное несмачивание (θ = π).

Необходимо отметить, что понятия смачиваемости и несмачиваемости поверхности твёрдого тела являются относительными и относятся к паре " жидкость – твёрдое тело ".

При смачивании или несмачивании поверхности твёрдого тела жидкостью, возможны различные варианты искривления поверхности жидкости.

Если поверхность жидкости не плоская, а искривлённая, то она оказывает на объём жидкости некоторое добавочное давление. Это давление, обусловленное силами поверхностного натяжения, для выпуклой поверхности будет положительным, а для вогнутой поверхности – отрицательным.

Для сферической поверхности избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривизной поверхности жидкости, может быть найдено по формулам:

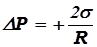, (17.20)

- для выпуклой поверхности, и

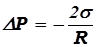, (17.21)

- для вогнутой поверхности.

Для вогнутой поверхности жидкости результирующая сила поверхностного натяжения направлена из жидкости. Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе (паре) на величину Δ Р.

Формулы (17.20) и (17.21) являются частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

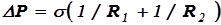, (17.22)

где R₁ и R₂ – радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в данной точке. Радиус кривизны считается положительным, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицательным, если центр кривизны находится вне жидкости.

Дата добавления: 2014-01-20