Выбор индексной формулы для расчета динамики физического объема и цен. Дефлятор ВВП

В наиболее общей форме для исчисления показателей динами­ки физического объема и цен на уровне экономики в целом ис­пользуются индекс физического объема ВВП и дефлятор ВВП. Индекс физического объема ВВП рассчитывается путем деле­ния стоимости ВВП в текущем периоде, оцененной в ценах ба­зисного периода, на его стоимость в базисном периоде:

(1)

где I_q^ВВП — индекс физического объема ВВП;

Σq_tp_o— стоимость ВВП в текущем периоде в ценах базисного

периода;

Σq₀p_o — стоимость ВВП в базисном периоде.

Дефлятор ВВП, характеризующий среднее изменение цен в экономике за определенный период, получают путем деления индекса стоимости ВВП (в текущих ценах) на индекс физическо­го объема ВВП или путем деления стоимости ВВП в текущем периоде на его стоимость в текущем периоде, оцененную в ценах базисного периода:

(2)

При исчислении индексов физического объема и дефляторов могут использоваться и другие индексные формулы (индексы И. Фишера, Торнквиста и др.). При выборе индексных формул используют аксиоматическую и экономическую теории индек­сов.

Аксиоматическая (формальная) теория индексов исходит из того, что индексная формула должна обеспечивать выполнение определенного набора аксиом (идентичности, монотонности, ад­дитивности, циркулярности, обратимости факторов во времени и др.) при ее применении.

Выполнение аксиомы идентичности означает, что если в отчет­ном периоде по сравнению с базисным ни одна цена не измени­лась, то сводный индекс цен равен 1 (100%). Действие аксиомы монотонности означает, что сводный индекс цен принимает зна­чение меньше или больше 1, если при сохранении уровня всех других цен цена /-го товара снижается (увеличивается). Приме­нительно к пересчету показателей в постоянные цены соблюде­ние принципа аддитивности означает, что сумма элементов в по­стоянных ценах должна быть равна итогу в постоянных ценах, а выполнение принципа циркулярности — что произведение цепных индексов должно равняться базисному индексу. Соблюдение тре­бования обратимости во времени означает, что расчеты динамики индексов цен не должны зависеть от выбора базы сравнения, что обеспечивается применением формулы средней геометрической. В математической форме требование обратимости во времени можно представить следующим образом:

I_t/0 ^. I_0/t = 1 (3)

Где I_t/0 – индекс цен в отчетном периоде по сравнению с базисным

I_{0/t -} индекс цен в базисном периоде по сравнению с отчетным

Важным также является требование обратимости факторов, в соответствии с которым произведение индексов цен и физического объема должно быть равно индексу стоимости. Аксиоматический подход позволяет различать только выполня­ющиеся и не выполняющиеся аксиомы; при этом вполне возмож­но, что довольно бессмысленные с экономической точки зрения ин­дексы выдержат все требования аксиоматической теории индексов. Еще один недостаток аксиоматической теории индексов — частое оперирование ценой и количеством как независимыми переменны­ми, хотя в действительности между ними существуют взаимосвя­зи, описание которых является задачей экономической теории.

Экономическая теория индексов предполагает существование «истинного» индекса, основанного на концепции «экономической полезности». По отношению к индексу потребительских цен это означает расчет «истинного индекса стоимости жизни», базирую­щегося на модели домашнего хозяйства, которое руководствуется извлечением максимальной пользы при выборе товаров и услуг. Это проявляется, в частности, в замещении одного товара (услу­ги) на другой (другую) вследствие изменения соотношения цен между ними.

По мнению авторов СНС-93, индекс цен по формуле Фишера (см. далее) при определенных условиях апроксимирует «истинный индекс стоимости жизни». Однако некоторые авторы полагают, что ввиду субъективного характера «полезности» и трудностей установления на практике этой категории экономическая теория индексов имеет ограниченное значение. Индексы цен используются для:

1) изучения динамики цен;

2) переоценки показателей в постоянные цены.

Для изучения динамики цен наиболее приемлемым является индекс цен по формуле Ласпейреса, при исчислении которого в ка­честве весов используются количественные данные базисного пе­риода:

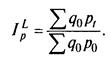
(4)

Индекс цен Ласпейреса показывает, насколько дороже или де­шевле стал фиксированный набор товаров (услуг) базисного пе­риода по сравнению с текущим.

Для переоценки показателей в постоянные цены наиболее при­емлемой в теоретическом отношении является формула индекса цен Пааше:

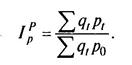
(5)

Индекс цен по формуле Пааше показывает, насколько дороже или дешевле стал набор товаров и услуг в текущем периоде по сравнению с базисным. При расчетах по этой формуле использу­ются текущие веса, т.е. структура набора товаров и услуг текуще­го периода.

Использование индекса цен Пааше с целью перехода от сто­имости агрегата в текущих ценах к его стоимости в ценах базис­ного периода (т.е. к оценке физического объема) аргументирует­ся, в частности, тем, что индексы физического объема определя­йся, как правило, по формуле Ласпейреса. При делении индекса стоимости на индекс цен Пааше получается связанный с ним индекс Физического объема Ласпейреса. Таким образом, использо­вание индекса цен Пааше позволяет увязать индексы стоимости, Физического объема и цен:

(6)

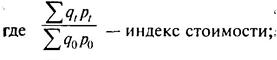Важным аргументом в пользу применения индекса цен Паше в качестве дефлятора является и то, что с его помощью может быть достигнута аддиктивность, т.е. существующие для показателя стоимости взаимосвязи сохраняются и для показателя физического объема.

Таким образом, индекс цен по формуле Паше соответствует принципам дефлятирования стоимостных агрегатов в СНС, поскольку рассчитанный с его использованием индекс физического объема удовлетворяет следующим требованиям:

- он представляет среднюю из индивидуальных индексов физического объема с постоянными весами;

- в нем элиминировано влияние цен, т.е. пока база остается неизменной, колебания цен в следующих за базисным периодах не оказывают влияния на индекс.

Несмотря на явные преимущества индексов цен Паше по сравнению с индексами цен Ласпейреса, в ряде случаев при отсутствии индексов цен Паше по практическим причинам используются индексы цен по формуле Ласпейреса.

Индекс Ласпейреса завышает измерение «истинного» значения теоретического индекса цен, тогда как индекс Паше – занижает то, что называется «эффектом Гершенкрона».

Для устранения этого эффекта компромиссным решением, рекомендуемым СНС-93, является использование для дефлятирования компонентов ВВП индекса цен по формуле Фишера, исчисляемого как средняя геометрическая из индексов Ласпейреса и Пааше:

(7)

Задача 5.2: СТАТИСТИКА И РАСЧЕТ ЦЕН В СНС-93

Дано: Определить соотношение цен продукции в системе СНС-93 с учетом налогов, надбавок и субсидий при ее движении от производства к конечному потребителю (млрд. у.е.). Определить цены факторные - Ц_ф, основные Ц_осн, цены производителя Ц_пр с учетом цен конечного покупателя (рыночных) Цкп и других показателей формирующих (определяющих) соответствующий уровень цен:

Цена конечного потребителя Цкп 280

НДС 30

Налоги на импорт НИ 10

Торгово-транспортные надбавки ТТН 20

Другие налоги на продукты (акцизы, продажи) ДНПрод 40

Субсидии на продукты СПрод 8

Другие налоги на производство ДНПроизв 12

Другие субсидии на производство ДСПроизв 5

(К_в = N_сп +10; прибавить Кв + Цкп)

Решение:

Ц_пр = Ц_кп -НДС – НИ – ТТН = 280 -30 -10 – 20 = 220;

Ц_осн = Ц_пр – ДНПпрод +СПпрод = 220 – 40 + 8 = 188;

Ц_ф = Ц_осн – ДНПроизв +ДСПпроизв = 188 – 12 + 5 = 181.

Лекция 6: СТАТИСТИКА И СИСТЕМА ОСНОВНЫХ СЧЕТОВ СНС-93 47с

Дата добавления: 2014-01-20