Формула полной вероятности. Формула Байеса

Теорема 1. Пусть событие A может произойти только с одним из несовместных событий (гипотез) , образующих полную группу, т.е. 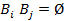при и . Тогда имеет место формула полной вероятности (ФПВ):

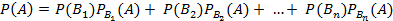(1.10)

Доказательство. По условию теоремы событие, где события 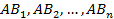несовместны. Тогда

.

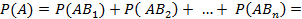
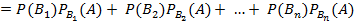Пример 1.15. Электролампы изготавливаются на трёх заводах. Первый завод изготавливает 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трёх заводов. Какова вероятность, что купленная в магазине лампа окажется стандартной?

Решение. Введём обозначения: купленная лампа изготовлена на первом заводе, лампа со второго завода, 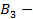лампа с третьего завода и, наконец, событие A – лампа оказалась стандартной.

Из условия задачи следует, что:

, , ,

, , .

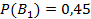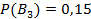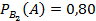По формуле полной вероятности (1.10):

Теорема 2 (формула Байеса). Пусть событие A может произойти только с одним из несовместных событий , образующих полную группу. Тогда:

или

Формула полной вероятности и формула Байеса связаны между собой и дают прямое и обратное решения одной проблемы. Прямая задача прогнозирует появление события A по известным до опыта вероятностям осуществления каждой гипотезы , а обратная дает переоценку вероятностей гипотез после того, как событие A произошло.

Пример 1.16. Завод-изготовитель прибора оценивает его надежность в 95%, а исследовательская лаборатория определяет надежность 80%. Путем эксперимента, проведенного потребителем, требуется установить, какой характеристике следует отдать предпочтение.

Решение. A – событие, состоящее в том, что прибор выдержал испытание, – противоположное событие. Если – события, состоящие в том, что верны данные соответственно завода и лаборатории, то

Естественно положить, что

Тогда

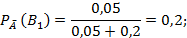
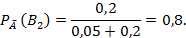
Только одна из найденных вероятностей относительно большая, это 0,8. Следовательно, если прибор не выдержал испытание, можно отдать предпочтение оценке, данной лабораторией.

1.24. Игра «последний герой». Каждому игроку дано по 2 белых и 2 черных камня и предложено разложить по двум непрозрачным сосудам произвольным образом. Ведущий наугад выбирает сосуд и наугад выбирает из него шар. Если шар белый – игрок остается в игре, если черный – покидает игру. Как нужно разложить шары по двум сосудам, чтобы иметь наибольший шанс остаться в игре?

Указание. Шары можно разложить одним из следующих способов:

Рассмотрите другие способы и найдите вероятность вынуть белый шар в каждом случае. Большая вероятность подскажет правильный вариант.

1.25. Литьё в болванках поступает из двух заготовительных цехов.: 70% из первого и 30% из второго. При этом продукция первого цеха имеет 10% брака, а второго – 20%. Найти вероятность того, что взятая наугад болванка без дефекта.

1.26. В трёх урнах находятся белые и черные шары: в первойурне 2 белых и 4 чёрных шара, во второй –3 белых и 5 чёрных, в третьей – 4 белых и 6 чёрных шаров. Из первой урны взяли наудачу 2 шара и переложили во вторую. После этого взяли 2 шара из второй урны и переложили в третью. Наконец, из третьей урны в первую переложили 2 шара. Найти вероятность событий: а) состав шаров во всех урнах не изменился; б) состав шаров во всех урнах не изменился.

1.27. Некто, заблудившись в лесу, вышел на поляну, откуда вело 5 дорог. Известно, что вероятности выхода из леса за час для различных дорог равны соответственно: 0,6; 0,3; 0,2; 0,1; 0,1. Чему равна вероятность, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса через час? ответы. 1.24. 2/3. 1.25. 0,87. 1.26. а) 173/495. Б) 0,094. 1.27. 6/13.

Дата добавления: 2014-01-20