
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Стокса
|
|
|
|
Для ламинарного режима ( ) и шарообразной формы тела аналитическая формула для силы сопротивления получена ученым Стоксом и носит название формулы Стокса:
) и шарообразной формы тела аналитическая формула для силы сопротивления получена ученым Стоксом и носит название формулы Стокса:
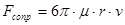 , (9)
, (9)
где 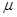 - коэффициент динамической вязкости среды;
- коэффициент динамической вязкости среды; 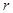 - радиус шара;
- радиус шара; 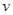 - его скорость относительно потока среды. Итак, формула, или закон, Стокса получена для медленного поступательного движения шара в неограниченной вязкой среде. Законом Стокса пользуются в коллоидной химии, молекулярной физике, физике аэрозолей. По закону Стокса можно определить скорость осаждения мелких капель тумана, частиц ила, коллоидных и аэрозольных частиц. Условие его применения:
- его скорость относительно потока среды. Итак, формула, или закон, Стокса получена для медленного поступательного движения шара в неограниченной вязкой среде. Законом Стокса пользуются в коллоидной химии, молекулярной физике, физике аэрозолей. По закону Стокса можно определить скорость осаждения мелких капель тумана, частиц ила, коллоидных и аэрозольных частиц. Условие его применения:  .
.
Определим предельную скорость при падении частицы, если сила сопротивления определяется формулой Стокса.
Сила тяжести равна  , где
, где  - объем и плотность материала частицы; подъемная сила равна
- объем и плотность материала частицы; подъемная сила равна 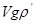 , где
, где 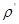 - плотность среды. Подъемная сила и сила сопротивления направлены противоположно скорости падения, а для установившегося движения сумма всех действующих сил равна нулю. Отсюда
- плотность среды. Подъемная сила и сила сопротивления направлены противоположно скорости падения, а для установившегося движения сумма всех действующих сил равна нулю. Отсюда
 .
.
Подставив выражение для объема частицы 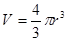 , получим
, получим
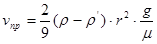 . (10)
. (10)
Если речь идет о падении шарика в воздухе, то плотностью воздуха можно пренебречь по сравнению с плотностью материала шарика, однако при падении в более плотных средах (например, в воде) формулу (10) следует использовать в полном виде. Порядки величин динамической вязкости для разных сред таковы:
| Среда | 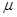 , мПа·с , мПа·с
|
| Воздух | 0.0182 |
| Вода | 1.002 |
| Глицерин |
Оценки показывают, что при расчете скорости падения в воздухе формула Стокса справедлива лишь для частиц микронных размеров.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 620; Нарушение авторских прав?; Мы поможем в написании вашей работы!