Режим Y—X

В отличие от режима линейной развертки в этом режиме на входы Y и X могут поступать исследуемые сигналы различных форм. Генератор развертки при этом не используется.

УЭ 4.2-4 Метод эллипса. В режиме круговой (эллиптической) развертки на входы Y и X ЭЛО подаются синусоидальные сигналы одной частоты или разных частот. На рисунке 4.9 приведен пример формиро­вания изображения при поданных на пластины Y и Х двух синусо­идальных напряжений одной частоты, но сдвинутых друг относи­тельно друга на 90°.

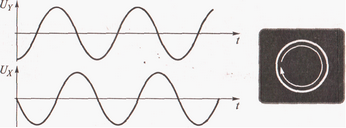
Рисунок 4.9 - Режим круговой развертки (режим Y—X)

Если на пластины Y и X поступают два синусоидальных сигнала одной частоты f = 1/T, но с некоторым сдвигом фаз t•360/T, то на экране ЭЛТ возникнет изображение наклоненного эллипса, по некоторым параметрам которого можно найти значение фазо­вого сдвига .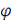

Измерив отрезки а и Ь, или с и d в изображении эллипса на экране, можно найти фазовый сдвиг φ, как показано на рисунке 4.10.

Рисунок 4.10 - Определение значения фазового сдвига

Поскольку sin φ = a/b, или sin φ = c/d, то значение фазового сдвига φ определяется таким образом: φ = arcsin(a/b) = arcsin(c/d).

На рис. 4.11 приведены примеры изображений для разных зна­мений фазового сдвига φ.

Рисунок 1.11. Изображения на экране в методе эллипса для разных значений

фазового сдвига: а — φ = 0°;б — φ = 30°; в — φ = 60°; г — φ = 90°; д — φ = 180°

УЭ 4.2 – 5 Метод фигур Лиссажу. Если на пластины Y и X поступают си­нусоидальные напряжения разных частот f_Y и f_x, то на экране ЭЛТ возникает изображение замкнутой фигуры — фигуры Лиссажу. На рисунке 4.12 показан случай формирования изображения, когда часто­та f_Y вдвое больше частоты f_x.

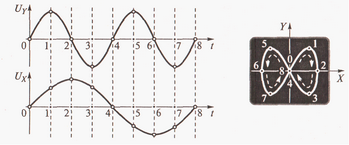
Рисунок 4.12 - Метод фигур Лиссажу

Зная значение одной из частот, можно найти значение другой. Этот метод используется для измерения неизвестной частоты си­нусоидальных сигналов. На один вход ЭЛО, например, на вход Y, подается сигнал неизвестной частоты, на другой — вход X — подается напряжение с выхода генератора синусоидальных сигналов. Изменением частоты сигнала генератора добиваются ус­тойчивого изображения на экране одной из понятных (удобных) фигур Лиссажу. Затем определяется число точек пересечения полу­ченной фигуры с горизонтальной и вертикальной линиями, как показано на рисунке 4.13, а. Для получения правильного результата линии должны проходить таким образом, чтобы число точек пересечения обе­ими линиями было максимальным. После этого отсчитывается значение установленной частоты сигнала генератора. Отношение частот f_Y/f_x равно отношению чис­ла точек пересечения по горизонтали N_T и по вертикали N_a: fr/fx=N_r/N_B.

На рис. 4.13, а приведен пример фигуры Лиссажу с соотноше­нием точек пересечения N_T/N_B = 6/4. Это значит, что частота сиг­нала на входе Y в полтора раза больше, чем частота сигнала на входе X. Например, если частота сигнала генератора, поданного на вход X, оказалась равной 12,4 кГц, то при такой фигуре на экране значение неизвестной частоты сигнала, поданного на вход Y, рав­но 18,6 кГц. Можно использовать и касательные к фигуре линии, как показано на рисунке 4.13, нотогда нужно использовать аналогичное соотноше­ние, но точек касания горизонтальной и вертикальной каса­тельной.

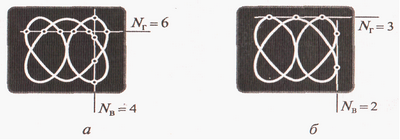
Рисунок 4.13 - Определение точек пересечения (а) или касания (б)

На рисунке 4.14 приведены примеры изображений для различных соотношений значений частот f_Y и f_x.

Рисунок 4.14 - Фигуры Лиссажу при соотношении частот fy/fx, равном: а - 3; б - 2; в - 3/2; г — 1; д — ½

Дата добавления: 2014-01-20