Лекция 5.2. Цифровые частотометры

Цифровые частотомеры — довольно распространенные изме­рительные приборы, используемые в самых различных отраслях науки, техники, промышленности для оценки частотно-временных параметров электрических сигналов. Они работают в очень широ­ком диапазоне значений измеряемых частот периодических сигналов (или их периода). Современные ЦЧ обеспечивают самые высо­кие метрологические характеристики (точность и разрешающую способность) среди всех прочих ЦИП, отличаются достаточно вы­соким быстродействием, широкими функциональными возмож­ностями, простотой эксплуатации, высокой надежностью.

Помимо измерения частотно-временных параметров периоди­ческих сигналов, современные ЦЧ применяются и для измере­ния различных физических величин. Для этого необходимо под­ключать к ЦЧ вспомогательные первичные измерительные пре­образователи (датчики), имеющие выходные сигналы, частота или период (длительность) которых пропорциональны измеряемой величине. Например, ЦЧ можно использовать для измерения ско­рости вращения вала двигателя, или расхода жидкости в трубо­проводе, или скорости потока воздуха. Цифровые частотомеры находят также применение в качестве генераторов стабильных частот и таймеров постоянных или программируемых интервалов времени. Кроме того, с помощью ЦЧ легко можно организовать подсчет числа импульсов (числа событий).

Практически все ЦЧ обеспечивают два основных режима рабо­ты: измерения частоты и измерения периода (длительности ин­тервала времени). Рассмотрим структуры, принципы действия и погрешности ЦЧ в этих режимах.
УЭ - 5.2.1. Режим измерения частоты

Упрощенная структура ЦЧ, реализующая режим измерения частоты, показана на рисунке 5.5, а, а временные диаграммы работы в этом режиме приведены на рисунке 5.5, б.

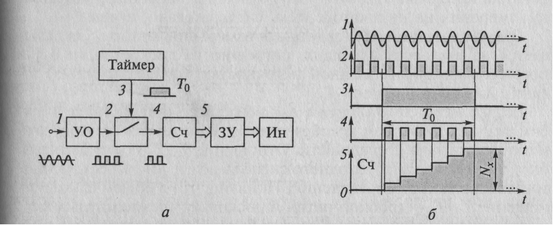
Рисунок 5.5. Режим измерения частоты: а — упрощенная структура ЦЧ; б — временные диаграммы работы

Исследуемый периодический сигнал 1 (соответственно диаг­рамма 7) подается на вход усилителя-ограничителя УО, где пре­образуется в последовательность прямоугольных импульсов 2 (диаграмма 2) фиксированной амплитуды, частота которых равна часто­те f_x входного сигнала. Далее этот сигнал поступает на вход электрон­ного ключа, которым управляет таймер, периодически замыкающий его на постоянный стабильный интервал времени 3 (диаграмма 3), например Г₀ = 1 с. Сформированная таким образом серия импульсов 4 (диаграмма 4) поступает на вход счетчика Сч, содержимое которого 5 в начале интервала Г₀ равно нулю, а в конце интервала счета равно числу поступивших импульсов N_x. Это число прямо пропорционально измеряемой частоте /_х входного сигнала:

N_x=Ent[T₀/T_x]= Ent[T₀f_x],

где Ent [...] — оператор определения целой части выражения [...]; Т_х — период входного сигнала (Т_х = 1/f_x); f_x — частота входного сигнала.

Содержимое счетчика 5 запоминается в буферном запоминаю­щем устройстве ЗУ и хранится там до окончания следующего цик­ла измерения и переписи нового результата. Одновременно результат поступает на цифровое отсчетное устройство (индикатор Ин). Если, например, в течение интервала Г₀ = 1 с на вход счетчика поступи­ло 254 импульса, то, следовательно, частота входного сигнала f_x = = 254 Гц. Прибор работает циклически, т.е. в начале каждого ново­го цикла счетчик «обнуляется». Таким образом, результат измере­ния периодически обновляется. Отметим, что форма периодичес­кого сигнала значения не имеет.

В реальных ЦЧ имеется несколько диапазонов измерения часто­ты, т. е. формируется несколько различных по длительности стабиль­ных интервалов T₀ (например,T₀₁ = 0,1 с; T₀₂ = 1,0 с; T₀₃ = 10 с). При работе с ЦЧ в режиме измерения частоты важным является правильный выбор диапазона, т. е. выбор интервала T₀, в течение которого происходит подсчет импульсов. Чем больше импульсов N_x поступит в счетчик (в пределах, конечно, максимально возмож­ного) на интервале T₀, тем больше будет значащих цифр результа­та измерения на индикаторе, тем, следовательно, лучше.

Общая погрешность Δ_F результата измерения частоты f_x склады­вается из двух составляющих: погрешности дискретности Δ_F1 и погрешности Δ_F2, вызванной неточностью (неидеальностью) за­дания интервала времени T₀.

Погрешность дискретности Δ_F1 неизбежно присутствует в лю­бом аналого-цифровом преобразовании. Рассмотрим природу воз­никновения этой погрешности. Отношение Т₀/Т_х может быть лю­бым, так как частота f_x входного сигнала может иметь бесконечное множество различных значений. Понятно, что в общем случае от­ношение Т₀/Т_х — дробное число. А поскольку число импульсов N_x, подсчитываемых счетчиком, может быть только целым, то в про­цессе такого автоматического округления естественно и неизбеж­но возникает погрешность (погрешность дискретности).Оценим возможное значение этой погрешности. При одном и том же постоянном значении интервала T₀, в зависимости от рас­положения (случайного) во времени входного сигнала и интерва­ла T₀, число импульсов, приходящихся на интервал T₀, может отличаться в ту или другую сторону на единицу. На рисунке 5.6, а показаны две разные ситуации при совершенно одинаковых ис­ходных условиях (одна и та же входная частота f_x, один и тот же интервал T₀): в первом случае (диаграмма 1) число импульсов, поступивших в счетчик, равно пяти, а во втором (диаграмма 2) случае число импульсов равно шести.

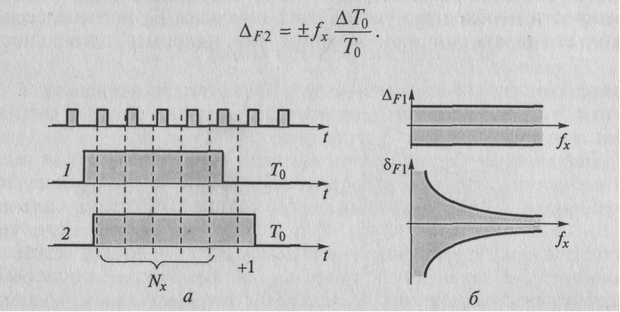
Рис. 5.6. Аддитивная погрешность в режиме измерения частоты: а — возникновение; б — абсолютная и относительная погрешности

Погрешность Δ_F1 — случайная величина, поскольку входной сигнал и сигнал таймера в общем случае никак не связаны между собой. Максимально возможное значение этой погрешности неиз­менно и составляет одну единицу младшего разряда — один квант:

Δ_F1 = ±1 импульс = ±1/T₀.

Таким образом, Δ_F1 — это аддитивная погрешность, т.е. не зависящая от значения измеряемой величины — частоты f_x , как показано на рисунке 5.6 б.

Погрешность Δ_F2 вызвана неточностью (неидеальностью) зада­ния интервала T₀ (см.рис. 5.6, а).

Если бы длительность интервала T₀ имела строго номинальное значение, то число импульсов, поступивших в счетчик, было бы равно N₁ (см. рис. 5.6, а). Если же интервал T₀ будет, например, несколько больше номинального и составит T₀ + ΔT ₀, то при той же измеряемой частоте f_x в счетчик поступит больше импульсов N₂ > N ₁ (см. рис. 5.6, а).

Неточность ΔT ₀ задания этого интервала приводит к появлению мультипликативной, т. е. линейно зависящей от значения из­меряемой частоты f_x, составляющей, что показано на рисунке 5.7 а и б

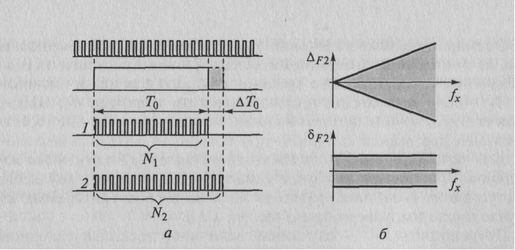
Рисунок 5.7. Мультипликативная погрешность в режиме измерения частоты: а — возникновение; б — абсолютная и относительная погрешности

Суммарная абсолютная погрешность Δ _F результата измерения частоты f_x и суммарная относительная погрешность δ_F, %, равны, соответственно:

Δ_F = Δ_F1+ Δ_F2 =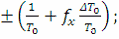

δ_F = δ_{F 1+} δ_{F 2} =

Графическая иллюстрация поведения составляющих и суммар­ных абсолютной и относительной погрешностей результата изме­рения частоты f_x приведена на рисунке 5.8, а и б, соответственно.

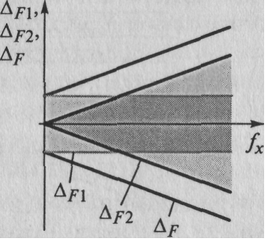
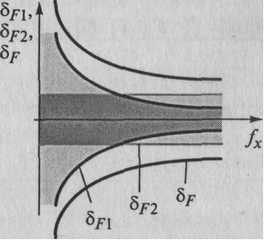
Рисунок 5.8. Суммарные абсолютная (a) и относительная (б) погрешности

Видно, что чем меньше значение измеряемой частоты f_x в этом режиме, тем (при постоянном интервале T₀) хуже, так как тем больше относительная погрешность δ_F. Для уменьшения этой по­грешности необходимо увеличивать интервал Т₀, но нецелесооб­разно его делать слишком большим. Так, например, длительность интервала Т₀ = 10 с уже неудобна для работы, так как значитель­ное время ожидания появления каждого нового результата (10 с) может вызвать у оператора раздражение. Для измерения сравни­тельно низких частот удобнее использовать второй режим ЦЧ — режим измерения периода (см. ниже) исследуемого входного сиг­нала Т_х = 1/ f _х. Рассмотрим пример определения погрешностей результата из­мерения частоты. Предположим, известны значение интервала Т₀ = = 1 с и возможная погрешность его задания ΔT ₀ = ±2 мс. Получен результат измерения частоты f_x = 1 кГц. Оценим значения состав­ляющих и суммарной погрешности результата.Значения абсолютных аддитивной Δ_F1 и мультипликативной Δ _F2 погрешностей, соответственно равны:

Δ_F1 = ±1/Т₀ = ±1 Гц;

Δ_{F 2=}

Значения относительных аддитивной δ_F1 и мультипликативной δ_F2 погрешностей определим обычным образом:

δ_F1 = (Δ_F1 /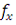)100 = ±(1/1000) 100 = ±0,1 %;

δ_F2 = (Δ_F2 /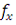)100 = ±(2/1000) 100 = ±0,2 %;

Суммарные абсолютная Δ_F иотносительная δ_F погрешности ре­зультата измерения частоты f_x соответственно равны:

Δ_F = Δ_F1 + Δ_F2 = ±3 Гц;

δ_F = δ_F1 + δ_F2 = ±3 %.

Дата добавления: 2014-01-20