
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ДМ. Лекция №6
|
|
|
|
Пример 14.
Доказательство.
Доказательство.
Следствие. Пусть R – отношение эквивалентности на множестве А, тогда
1) (Î А) Α Î /R.
2) = A.
3) (,b Î А) /R = b/R Û R b.
4) /R ≠ b/R Û /R ∩ b/R = Æ.
Пусть S – разбиение непустого множества А и - бинарное отношение, определяемое следующим образом: (x,y) Îтогда и только, когда x и y принадлежат одному и тому же подмножеству семейства S.
Теорема 3. (обратная теореме 1). Отношение соответствующее разбиению S непустого множества А, является отношением эквивалентности на А, причём фактор- множество А/ совпадает с разбиением S.
Замечание 3. Частный случай отношения эквивалентности – отношение равенства определяет разбиение множеств на одноэлементные классы эквивалентности
, то есть классов оказывается столько же, сколько элементов содержится в множестве А (каждый элемент из А эквивалентен только самому себе). Другой крайний случай заключается в том, что все элементы А объявляются эквивалентными друг другу, при этом разбиение множества А состоит всего из одного класса – самого множества А. В любом другом случае среди классов разбиения имеется хотя бы один класс, который содержит больше одного элемента и в то же время не совпадает с самим множеством А.
Замечание 4. В чём важность такого разбиения множества на классы? Дело в том, что в каждом классе эквивалентности оказываются эквивалентные элементы, то есть элементы, неразличимы с точки зрения некоторого отношения. Например, равные отрезки или подобные треугольники. Поэтому считают, что класс эквивалентности (множество) определяется любым своим представителем, то есть произвольным элементом этого класса. Так, класс равных отрезков можно задать, указав любой отрезок, принадлежащий этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность отдельных представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, определяется разбиением этого множества на классы треугольников, четырёхугольников, пятиугольников и так далее. Свойства, присущие некоторому классу, рассматриваются на одном его представителе.
Важную роль играют отношения эквивалентности в определении математических понятий.
Тема: «Алгебраические структуры»
Для моделирования кибернетических систем важнейшую роль играют алгебраические структуры. Эти структуры позволяют описывать дискретное строение таких систем и дискретность функционирования таких систем.
def. Множество М вместе с набором операций 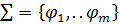 ,
, 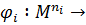 M, где ni - рангом операции
M, где ni - рангом операции 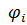 , называется алгебраической структурой, универсальной алгеброй или просто алгеброй.
, называется алгебраической структурой, универсальной алгеброй или просто алгеброй.
Множество М называется основным (несущим) множеством или основой (носителем); упорядоченная последовательность рангов (n1,…, nm) называется типом; множество операций S называется сигнатурой.
Запись: < М; S > или < М;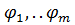 >. Операции
>. Операции 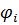 конечноместны, сигнатура S конечна. Носитель необязательно конечен, но не пуст.
конечноместны, сигнатура S конечна. Носитель необязательно конечен, но не пуст.
Замечание. Далее для обозначения алгебры везде, где это возможно, используется прописная рукописная буква, а для обозначения ее носителя – соответствующая печатная прописная буква:
А = < A, S >.
def. Алгебры А = < A, f1, …, fs > и В = < В,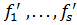 > называются однотипными, если их типы совпадают, то есть ранг операции
> называются однотипными, если их типы совпадают, то есть ранг операции 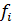 совпадает с рангом соответствующей ей операции
совпадает с рангом соответствующей ей операции
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 331; Нарушение авторских прав?; Мы поможем в написании вашей работы!