Лекция №8. Криволинейный интеграл I рода

Криволинейный интеграл I рода.

Определение. Пусть на дуге АВ кусочно-гладкой кривой задана функция (скалярное поле). Разобьём дугу АВ на n частей (элементарных дуг), длины которых 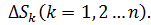Разметим дугу, то есть выберем на каждой элементарной дуге точку . Составим интегральную сумму

k

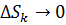Предел этой суммы при max называется криволинейным интегралом рода от функции по кривой АВ (при условии, что предел существует и не зависит от способа разбиения и разметки). Обозначение интеграла:

(1)

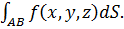
Кроме свойств линейности и аддитивности криволинейный интеграл I рода (в отличие от интеграла II рода), обладает следующим свойством:

он не зависит от того, в каком направлении проходит дуга АВ (Этим свойством объясняется наличие модуля в формулах (2)-(4)).

Физически интеграл (I) представляет собой массу кривой AB линейной плотностью . Если 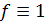, то интеграл равен длине дуги AB.

Вычисление интеграла (I) сводится к вычислению определенного интеграла:

(2)

гдепараметрические уравнения кривой AB,

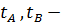параметрические координаты точек А и В.

Если 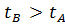, то модуль в формуле (2) можно опустить.

В случае плоской кривой АВ с уравнением из формулы (2) заменой получим:

(3)

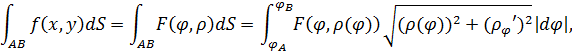
где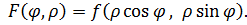

Пример1. Дуга АВ параболы 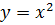, 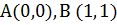является направляющей цилиндрической поверхности. Найти площадь этой поверхности, заключенной между плоскостями .

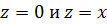Решение. Применяем формулу (3):

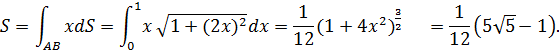
Пример 2. Найти момент инерции однородной окружности радиуса R и массы М относительно диаметра.

Решение. Найдем линейную плотность кривой

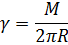
Запишем параметрически уравнения окружности С

и момент инерции относительно оси X

Интеграл вычислим по формуле (2)

Криволинейный интеграл II рода.

Определение. Пусть на дуге АВ кусочно-гладкой кривой задана векторная функция (векторное поле):

. (5)

Разбиение дуги АВ на элементарные и ее разметку выполним также, как для интеграла I рода. Концы каждой элементарной дуги соединим вектором
∆ . Составим интегральную сумму скалярных произведений:

  (6)

k

Предел этой суммы при max называется криволинейным интегралом II рода от функции (или линейным интегралом векторного поля) по кривой АВ (при условии, что предел существует и не зависит от способа разбиения и разметки). Обозначения интеграла:

Физически интеграл (6) представляет собой работу переменной силы (5) на криволинейном пути АВ в заданном направлении, то есть от точки А до точки В.

Вычисление интеграла (6) также сводится к вычислению определенного интеграла. Для параметрически заданного пути АВ формула имеет следующий вид:

  (8)

(7)

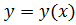Для плоской задачи и уравнения кривой АВ в явной форме , считая 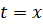из формулы (7) получим:

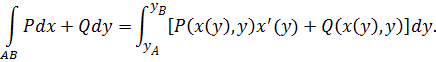
Пример 3. Вычислить интеграл

по следующим путям:

а) по прямой АВ,

б) по ломаной АОВ, где О(0,0),

в) по дуге окружности с центром О.

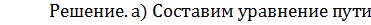
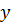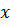Отсюда , то есть выражаем через и, следовательно, пределы необходимо расставить по 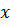от

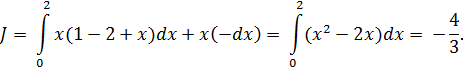
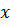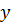б) В этом случае путь интегрирования состоит из двух звеньев. Используя свойства аддитивности, разбиваем интеграл на сумму двух интегралов по путям АО и ОВ. Для первого интеграла уравнение пути . Отсюда . Таким образом, выразим через и, следовательно, пределы необходимо расставить по 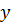от . Для второго интеграла уравнение пути , то есть и пределы от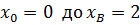

в) Уравнение окружности запишем в параметрическом виде

Отсюда 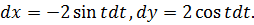Пределы по от

Приведенный пример иллюстрирует зависимость величины интеграла от пути интегрирования.

Формула Грина.

  (10)

Для плоского случая криволинейный интеграл по замкнутому контуру можно свести к двойному интегралу по формуле Грина

При этом необходимо выполнение следующих условий:

1) функции 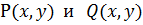вместе с частными производными

должны быть непрерывны в замкнутой области , то есть в односвязной области, ограниченной замкнутой кривой .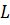

2) направление обхода пути 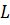положительное, то есть при движении по кривой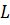в этом направлении, область должна оставаться с левой стороны.

Криволинейный интеграл от полного дифференциала.

Подынтегральное выражение является полным дифференциалов некоторой функции при условиях:

1) функции непрерывны

2) 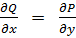. (11)

Если выполняются эти условия, то криволинейный интеграл по любому замкнутому контуру равен нулю (это следует из формулы (10)), а криволинейный интеграл по пути АВ не зависит от выбора пути. Это позволяет упростить вычисление интеграла, благодаря выбору удобного пути: ломаная со звеньями, параллельными осям координат.

Если известна первообразная , то криволинейный интеграл от полного дифференциала можно вычислить по формуле, аналогичной формуле Ньютона-Лейбница

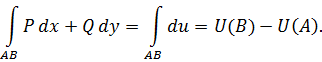
Пример 4. Вычислить ,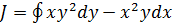

где - окружность , проходимая в положительном направлении.

Решение. Обозначим через круг . С помощью формулы Грина получим:

Полученный интеграл легко вычисляется в полярных координатах

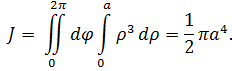
Пример 5. Вычислить

Решение. Такая запись криволинейного интеграла указывает на начало пути (точка 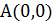) и конец (точка 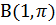). Проверяем условия (11). Они выполняются, следовательно, интеграл не зависит от пути, и можно рассматривать любой путь из точки 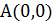в точку 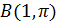. Наиболее выгодный из них - ломаная, состоящая из отрезков прямых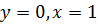

Пример 6. Вычислить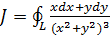

где 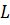– любой замкнутый контур, охватывающий точку 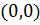. Направление обхода – против часовой стрелки (то есть положительное).

Решение. Проверяем условия (11). Второе условие выполняется, а первое условие в точке 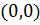не выполняется. Поэтому нельзя использовать формулу (10) и сказать, что 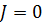. Но можно легко доказать, что интеграл 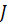не зависит от контура 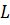(контур должен охватывать начало координат). Выберем в качестве контура окружность единичного радиуса

Для вычисления интеграла используем формулу (7)

Дата добавления: 2014-01-20