Частотный преобразователь

Вычисление ранга матрицы

1. Метод окаймляющих миноров (о нем было сказано выше)

Пример. Найдем Rang A.

Находим ненулевой минор второго порядка и окаймляющие его миноры третьего порядка:

;;

Отсюда получаем, что Rang A= 2.

2. Метод элементарных преобразований.

Элементарными преобразованиями строк назовем:

1) перестановку строк;

2) сложение строк;

3) умножение строки на число.

Теорема (без доказательства). Элементарные преобразования строк (столбцов) матрицы, а также транспонирование матрицы и вычеркивание нулевой строки (столбца) не меняют ранга матрицы. ▲

Матрицы вида

(*)

называются ступенчатыми, или трапециевидными.

Идея метода элементарных преобразований состоит в следующем. Приведем элементарными преобразованиями матрицу к ступенчатому виду, в котором

(**).

Очевидно, ранг матрицы вида (*) равен r, если выполнены условия (**). Тогда ранг и исходной матрицы равен r:

A = Rang A=r.

Пример. Найдем Rang A методом элементарных преобразований:

Решение:

вычеркиваем нулевую строку

Вычтем вторую строку из третьей

Вычтем первую строку из второй

Получаем ответ: Rang = Rang A =2.

Транзисторы работают в ключевом режиме. Диоды шунтируют транзисторы от пробоя при закрытии. Рассмотрим токи по обмоткам статора.

«1»- открытое состояние,

«0»- закрытое.

Время	VT1	VT2	VT3	VT4	VT5	VT6
t0-t1
t1 - t2
t2 - t3
t3 - t4
t4 - t5
t5 - t6
t6 - t7

Для вращения поля в обратную сторону необходимо изменить логику.

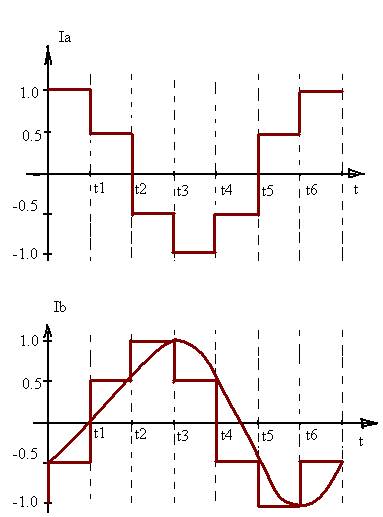
Управление частотой – то же, что и управление величиной Δt.

Токи не меняются скачком, а имеют плавное изменение (т.к. индктивная нагрузка).

Картина отражает изменение транзисторов.

(Рис.)

Диод при включении не работает, но накомпленная энергия при включении рассасывается через него.

Дата добавления: 2014-01-20