В1.1. Что такое метод математической индукции (ММИ)

Метод математической индукции

ЛЕКЦИЯ В1

Введение

Краткое содержание лекции

· Что такое метод математической индукции

· Примеры доказательств по методу математической индукции

Метод математической индукции – одно из мощных средств доказательства теорем.

Пусть P (n) - некоторое утверждение (формула, теорема), которое зависит от значения натурального n. Для некоторых n утверждение P (n) может быть ложным, для других – истинным. ММИ применяется для доказательства истинности P (n) для всех натуральных n, начиная, с некоторого n ₀ ³ 1.

Примеры утверждений P (n).

Пример 1. Если а ₁, …, а_п > 0, то 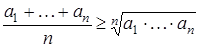(среднее арифметическое п положительных вещественных чисел не меньше их среднего геометрического). Это утверждение верно для всех п ³ 1.

Пример 2. Среди любых п натуральных чисел обязательно найдутся 2, разность которых делится на 1000. Это утверждение верно для любого п ³ 1001.

Пример 3. Сумма 7¹ + 7² + … +7 ^п делится на 100.

Это утверждение верно для п = 4, 8, 12, …, 4 m, … и ложно для остальных п.

Утверждения 1 и 3 доказываются ММИ. Утверждение 2 доказывается с помощью принципа Дирихле.

Доказательство истинности P (n) для всех п ³ п ₀ основано на принципе, который формулируется так.

Принцип индукции (классический принцип индукции). Пусть P(n) таково, что P(п₀) - истинное утверждение и из истинности P(k) следует истинность P(k+1). Тогда P(n) истинно для всех п ³ п₀.

Эквивалентная формулировка принципа индукции (расширенный принцип индукции):

1. Пусть P (n ₀) – истинное утверждение.

2. Из истинности P (n) для всех n = п ₀, п ₀+1, п ₀+2, …, k, следует истинность P (k +1).

Тогда P (n) истинно для всех n ³ п ₀.

Доказательство по методу математической индукции проходит в три этапа

· База индукции. Доказывается истинность .

· Шаг индукции или индуктивное предположение.

Допускается истинность утверждения P (k) (или P (n) для всех n ₀ £ п £ k).

· Вывод или индуктивный переход.

Доказывается истинность утверждения P (k +1), исходя из индуктивного предположения.

Замечание. Чаще всего база индукции начинается с n ₀ = 1.

На рис.1 приведена схема доказательства по методу математической индукции (для простоты положим, что база индукции начинается с n = 1).

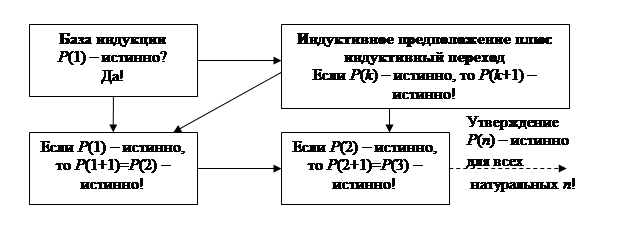
Рис. 1

Пример 1. Доказать при помощи метода математической индукции

.

Доказательство.

Дата добавления: 2014-01-20