Лекция 13. Тема:Операционное исчисление

Тема: Операционное исчисление.

13.1 Преобразование Лапласа.

Определение 1. Функцией – оригиналом называется комплексная функция f(t) действительного аргумента t, удовлетворяющая следующим условиям:

1) F(t) непрерывна вместе со своими производными достаточно высокого порядка на всей оси t, кроме отдельных точек, в которых f(t) или её производные терпят разрыв

1-го рода, причем на каждом конечном интервале оси t таких точек имеется лишь конечное число.

2) При t<0, f(t)=0

3) F(t) возрастает не быстрее показательной функции, т.е. существуют такие постоянные, M, , , 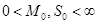что для всех t выполняется неравенство

Число называется показателем роста f(t), для ограниченных функций =0.

Простейшей функцией оригиналом является единичная функция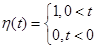

Если функция 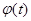удовлетворяет условиям 1) и 3), но не удовлетворяет условию 2), то произведение удовлетворяет всем условиям 1), 2), 3). Например, оригиналами будут функции 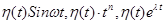и т.д. Для простоты записи множитель будем опускать, условившись, что все функции f(t), при t<0 равны 0. Например, вместо будем писать 1, вместо 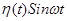будем писать 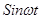и т.д.

Определение 2: Изображением функции f(t) по Лапласу называют функцию комплексного переменного , определенную отношением: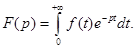

Фразу: «функция f(t) имеет своим изображением F(p)» будем записывать символом или .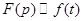

Пример 1: 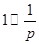. Действительно .

Пример 2: Имеем:

.

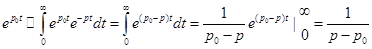Непосредственно из свойств интеграла получаем:

1. Свойство линейности.

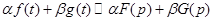, где .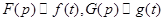

Пример 3: .

2. Теорема подобия.

. Доказательство. =

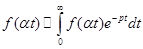В интеграле сделаем замену

= .

3. Дифференцирование оригинала.

Если или вообще 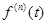является оригиналом, то или

, где под понимаем правое предельное значение .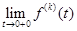

4. Дифференцирование изображения.

5. Интегрирование оригинала.

6. Интегрирование изображения.

, где путь интегрирования лежит в полуплоскости .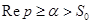

Пример 4. Найти изображение функции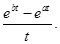

Из примера 2 и свойства 1 имеем: 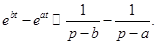Пользуясь свойством 6, получаем

.

Пример 5.

Пример 6.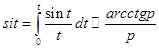

Таблица оригиналов и их изображений.

№	Оригинал	Изображение
(83,4)
(80,1)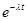
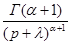
(80,3)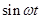
(80,4)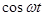
(80,12)
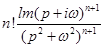
(80,12)
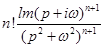
(80,22)
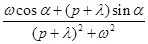
(80,22)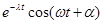
(80,4)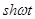
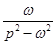
(80,4)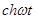
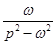
(80,15)
(83,5’)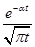

13.2 Решение обыкновенных дифуравнений с постоянными коэффициентами.

Решить дифуравнение с начальными условиями

1.

Решение. .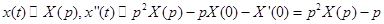

В данном дифуравнении переходим к изображениям.

. По таблице для X(p) находим оригинал х(t)=cost.

2. .

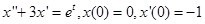Решение. ,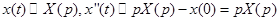

,

,

.

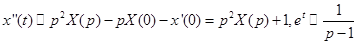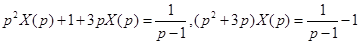Правильную рациональную дробь представим в виде суммы простейших рациональных дробей.

.

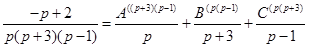После приведения левой и правой части равенства к общему знаменателю, приравниваем числители: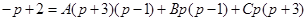

а) p=0, 2=-3A, A=-

б) p=-3, 5=12B, B=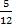

в) p=1, 1=4C, C=

.

Переходя к основному равенству получим:

Дата добавления: 2014-01-20