
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение
|
|
|
|


|

|

|

|

|

|

|

|

|

|

|

|

|

Рассмотрим теперь примеры линейных пространств функций. Сделаем сначала некоторые общие замечания. Пусть 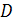 — некоторое множество элементов
— некоторое множество элементов 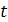 произвольной природы, и пусть каждому
произвольной природы, и пусть каждому 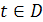 поставлен в соответствие элемент
поставлен в соответствие элемент  линейного пространства
линейного пространства  , т. е. задана функция
, т. е. задана функция  с областью определения
с областью определения 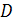 и с областью значений в
и с областью значений в  . Под суммой
. Под суммой  двух таких функций
двух таких функций  и
и  будем понимать функцию
будем понимать функцию  . Под произведением
. Под произведением  функции
функции  на число
на число  будем понимать функцию
будем понимать функцию 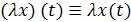 .
.
В предлагаемых ниже примерах рассматриваются функции с вещественными или комплексными значениями, т. е.  — вещественная ось или комплексная плоскость. Как и выше, операции над такими функциями сводятся к операциям над вещественными или комплексными числами. Фиксируя
— вещественная ось или комплексная плоскость. Как и выше, операции над такими функциями сводятся к операциям над вещественными или комплексными числами. Фиксируя 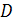 и выбирая тот или иной класс функций, мы автоматически получим выполнение аксиом линейного пространства, если только
и выбирая тот или иной класс функций, мы автоматически получим выполнение аксиом линейного пространства, если только  и
и  принадлежат выбранному классу функций вместе с
принадлежат выбранному классу функций вместе с 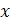 и
и  .
.
Пример 6. Рассмотрим пространство всех многочленов степени, не превышающей  :
:  (
( — произвольные вещественные числа,
— произвольные вещественные числа, 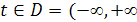 . Поскольку произведение многочлена на вещественное число и сумма двух многочленов являются многочленами, мы получаем линейное пространство многочленов.
. Поскольку произведение многочлена на вещественное число и сумма двух многочленов являются многочленами, мы получаем линейное пространство многочленов.
Точно так же можно рассмотреть комплексное линейное пространство многочленов степени не выше  . Его элементы
. Его элементы  имеют вид
имеют вид  (
( — комплексные числа,
— комплексные числа, 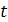 —комплексная переменная, изменяющаяся на комплексной плоскости
—комплексная переменная, изменяющаяся на комплексной плоскости 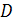 ).
).
Пример 7. Пространство непрерывных функций 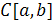 . Пусть
. Пусть  . Берем всевозможные непрерывные на
. Берем всевозможные непрерывные на  функции
функции 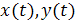 . Так как
. Так как  непрерывна на
непрерывна на  , как сумма непрерывных функций, и
, как сумма непрерывных функций, и 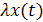 также непрерывна, то
также непрерывна, то 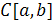 является линейным пространством. Возможны вещественный и комплексный случаи.
является линейным пространством. Возможны вещественный и комплексный случаи.
Пример 8. Пространство 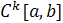 (
( — натуральное число) — пространство
— натуральное число) — пространство  раз непрерывно дифференцируемых функций. Поскольку
раз непрерывно дифференцируемых функций. Поскольку  , если
, если 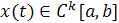 , и
, и 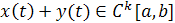 , если
, если 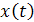 и
и  , то
, то 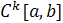 — линейное пространство.
— линейное пространство.
Пример 9. Рассмотрим множество  всех прямоугольных матриц порядка
всех прямоугольных матриц порядка 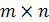 со скалярными элементами
со скалярными элементами
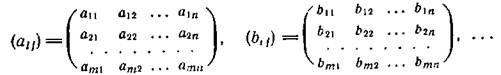
Определим в  операции
операции
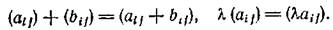
Поскольку операции над матрицами сводятся к операциям над числами, то справедливость аксиом очевидна. Если элементы матриц искаляры  вещественны (комплексны), то мы приходим к вещественному (комплексному) линейному пространству.
вещественны (комплексны), то мы приходим к вещественному (комплексному) линейному пространству.
В дальнейшем мы встретимся и с другими примерами линейных пространств.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 327; Нарушение авторских прав?; Мы поможем в написании вашей работы!