Действия над линейными операторами

Над линейными операторами, определяемыми в линейном пространстве, можно производить различные действия, приводящие к новым линейным операторам. Рассмотрим здесь действия сложения операторов, умножения на число и умножения операторов друг на друга.

1. Сложения линейных операторов

Пусть в пространстве 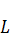заданы линейные операторы и .

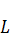Определение. Суммой операторов и в пространстве называется такой оператор , для которого выполняется равенство

где 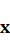– любой вектор из .

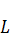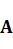Можно показать, что сумма линейных операторов является линейным оператором, причем его матрица равна сумме матриц и операторов и, то есть .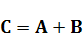

2. Умножение линейного оператора на число

Определение. Произведением линейного оператора на число называется оператор , определяемый равенством

где 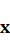– любой вектор из .

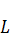Можно показать, что оператор является линейным оператором, а его матрица равна произведению числа на матрицу оператора 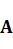, то есть .

3. Умножение линейных операторов

Применим к произвольному вектору 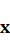из 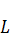сначала оператор , а затем оператор , получим вектор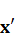

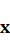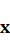Определение. Оператор , переводящий вектор непосредственно в , называется произведением оператора на оператор , т.е. для всех векторов из 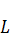имеет место равенство

при этом используется запись .

Можно показать, что произведение линейных операторов есть снова линейный оператор, а его матрица равна произведению матриц этих операторов, взятых в порядке, обратном действию операторов, то есть

4. Сопряженный оператор

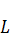Определение. Оператор называется сопряженным по отношению к оператору , если для любых векторов и из пространства выполняется равенство

Можно показать, что если оператор линейный, то у него существует единственный сопряженный оператор . При этом, если матрица

является матрицей оператора , то матрицей оператора . является матрица

Такая матрица называется сопряженной по отношению к матрице . При этом, если оператор действует из 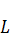в то .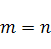

Можно показать, что имеет место следующая теорема.

Теорема (Альтернатива Фредгольма)

Пусть – линейный оператор, который действует из евклидова пространства на евклидово пространство , а – оператор, сопряженный по отношению к оператору .

Тогда или уравнение

где 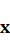и – произвольные векторы из , имеет единственное решение, или уравнение

имеет, по крайней мере, одно ненулевое решение.

Определение. Линейный оператор называется самосопряженным (или Эрмитовым), если он совпадает со своим сопряженным, т.е. если для любого вектора из выполняется равенство

Определение. Квадратная матрица называется симметричной, если для ее элементов выполняется равенство

Можно показать, что матрица самосопряженного оператора симметричная.

Дата добавления: 2014-01-20