Теорема умножения вероятностей. При изучении реальных случайных явлений иногда возникает или искусственно создается ситуация, когда мы получаем дополнительную информацию о возможных исходах

При изучении реальных случайных явлений иногда возникает или искусственно создается ситуация, когда мы получаем дополнительную информацию о возможных исходах испытания Ω.

Например, известно, что студент из 30 билетов успел выучить билеты с 1-го по 3-й и с 28-го по 30-й. На экзамен он пришел одиннадцатым, и оказалось, что к его приходу остались только билеты с 1-го по 20-й (событие В). Вероятность события А ={студент получил выученный билет} без дополнительной информации о том, что событие В произошло, может быть вычислена по классическому определению с Ω={1,2,…,30}. Согласно классической формуле имеем: . При дополнительной информации (событие В произошло) множество возможных исходов В состоит из 20 элементарных исходов, а событие А вместе с В наступает в 3 случаях. Следовательно, в рассматриваемом примере естественно определить условную вероятность.

Определение 1. Условной вероятностью называют вероятность события А, вычисленную в предположении того, что событие В уже произошло.

Таким образом, в рассматриваемом примере

Замечание. Понятие условной вероятности используется в основном в случаях, когда осуществление события В изменяет вероятность события А.

Пример 3. Пусть событие В – извлечение из колоды в 32 карты туза, а событие А – то, что и вторая вынутая из колоды карта окажется тузом. Тогда, если после первого раза карта была возвращена в колоду, то вероятность вынуть вторично туз не меняется: 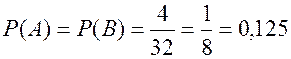. Если же первая карта в колоду не возвращается, то осуществление события В приводит к тому, что в колоде осталась 31 карта, из которых только 3 туза. Поэтому .

Пример 4. Если событие А – попадание в самолет противника при первом выстреле из орудия, а В – при втором, то первое попадание уменьшает маневренность самолета, поэтому P_A (В) увеличится по сравнению с P(А).

Теорема 2 (теорема умножения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

P (АВ) = P (А) · P_A (В). (7)

Доказательство. Воспользуемся обозначениями теоремы 1. Тогда для вычисления P_A (В) множеством возможных исходов нужно считать т_А (так как А произошло), а множеством благоприятствующих исходов – те, при которых произошли и А, и В (т_АВ).

Следовательно,, откуда следует утверждение теоремы.

Пример 5. Для поражения цели необходимо попасть в нее дважды. Вероятность первого попадания равна 0,2, затем она не меняется при промахах, но после первого попадания увеличивается вдвое. Найти вероятность того, что цель будет поражена первыми двумя выстрелами.

Решение. Пусть событие А – попадание при первом выстреле, а событие В – попадание при втором. Тогда P (А) = 0,2, P _A (В) = 0,4, P(АВ) = 0,2·0,4 = 0,08.

Следствие. Если подобным образом вычислить вероятность события ВА, совпадающего с событием АВ, то получим, что P (ВА) = P (В) · P_B (А). Следовательно,

P (А) · P_A (В) = P (В) · P_B (А). (8)

Определение 2. Событие А называется независимым от события В, если появление события В не изменяет вероятности события А, то есть P_B (А) = P (А).

Замечание. Если событие А не зависит от В, то и В не зависит от А. Действительно, из (8) следует, что P (А) · P_A (В) = P (В) · P (А) (т.к. А не зависит от В и P_B (А) = P (А)), откуда P_A (В) = P (В). Значит, свойство независимости событий взаимно.

Таким образом, из теоремы 2 и определения 2 следует теорема 3.

Теорема 3 (умножения независимых событий). Вероятность произведения двух независимых событий равна произведению их вероятностей.

P (АВ)= P (А)· P (В), (9)

то есть вероятность произведения независимых событий равна произведению их вероятностей.

Теорема умножения вероятностей легко обобщается на случай произвольного числа событий.

Следствие. Вероятность совместного проявления нескольких событий равна произведению вероятностей одного из них на условные вероятности всех остальных:

(10)

При решении задач теоремы сложения и умножения обычно применяются вместе.

Пример 6. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0,6 и 0,7. Найти вероятности следующих событий:

А – хотя бы одно попадание при двух выстрелах;

В – ровно одно попадание при двух выстрелах;

С – два попадания;

D – ни одного попадания.

Решение. Пусть событие Н ₁ – попадание первого стрелка, Н ₂ – попадание второго. Тогда

А = Н ₁ + Н ₂, , , 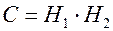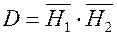. События Н₁ и Н₂ совместны и независимы, поэтому теорема сложения применяется в общем виде, а теорема умножения – в виде (8). Следовательно, P (С) = 0,6·0,7 = 0,42, P (А) = 0,6 + 0,7 – 0,42 = 0,88, P (B) = 0,6·0,3 + 0,7·0,4 = 0,46 (так как события и 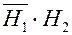несовместны), P (D) = 0,4·0,3 = 0,12. Заметим, что события А и D являются противоположными, поэтому P (А) = 1 – P (D).

Дата добавления: 2014-01-20