
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство применимости теории упругости к грунтам (постулаты теории упругости)
|
|
|
|
Напряженное состояние и прочность грунтов.
Постановка задачи
Доказательство применимости теории упругости к грунтам (постулаты теории упругости).
Напряженное состояние и прочность грунтов.
Постановка задачи
Определение напряжений в массиве грунта
Решение задачи определения напряжений в грунте необходимо для установления условий прочности и устойчивости грунтов и определения их деформаций (например, осадок). При решении вопроса о распределении напряжений в грунтах в механике грунтов применяют теорию линейно-деформируемых тел. То есть для определения напряжений могут быть применены уравнения и зависимости теории упругости, базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука). Однако при применении закона Гука для грунтов необходимо условиться об ограничениях, поскольку в грунтах возникают не только упругие, но значительные остаточные деформации.
Давление от внешних нагрузок в грунтовых массивах создает внутренние усилия. Величина напряжений характеризует их интенсивность. Грунтовые напряжения так же делятся на нормальные σ и касательные τ. Напряжение, возникающее в любой точке грунта σ является результатом суммарного действия сил: внешней нагрузки, собственного веса грунта, порового давления, капиллярного давления. Осадка зданий и сооружений не может быть решен без учета распределения напряжений в слоях грунта. В настоящее время для определения напряжений применяем аппарат теории упругости. При этом расчетные модели грунта - модель дискретной среды и модель сплошной среды, которая делится на модель линейно-деформируемой среды (ЛДС), упруго-пластической среды (УПС) и теории предельного равновесия (ТПР). Два основных постулата: концепция сплошности (грунт в процессе деформации остается неразрывной сплошной средой) и концепция равномерности з- все компоненты грунта равномерно распределяются по объему.
В на стоящее время в механике грунтов при определении напряжений в грунтовых массивах используют решение линейной теорию упругости. Для  применения этих решений приходиться принимать ряд допущений и ограничений.
применения этих решений приходиться принимать ряд допущений и ограничений.
а) Деформации пропорциональны напряжениям
 |

| Р
|
б)Теория упругости рассматривает тела упругие.
         Р Р
 Sост Sост
  Sупр. Sупр.
 S
S
| В грунтах наблюдаются большие остаточные деформации Sост. Но для строителей существенно одноразовое загружение основания, т.е. здесь условие упругости применимо (а в общем случае нет). |
в) Теория упругости рассматривает тела сплошные.

.
|
в точках контакта
частиц  - огромно (до 200 МПа) - огромно (до 200 МПа)
| В расчетах допускается использовать sср. - среднюю величину напряжений, действующих по определенной площадке. В этом случае можно говорить о «сплошности» грунтов. |
Следовательно, в расчётах механики грунтов, с учетом отмеченных допущений, можно использовать теорию упругости.

 5.4 Определение напряжений в массиве грунта от
5.4 Определение напряжений в массиве грунта от
сосредоточенной силы. (задача Буссинеско 1885 г.)
               Р Р
 0 0
 R R
 r M r M
 М1
Z М1
Z
| Определить значения вертикальных напряжений 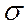 z и касательных напряжений; z и касательных напряжений;  ; ; 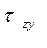 в точке М, расположенной на площадке параллельной плоскости ограничивающий массив. в точке М, расположенной на площадке параллельной плоскости ограничивающий массив.
|
Задачу решаем в 3 этапа:
1) О пределяем  R – в радиальном направлении
R – в радиальном направлении  R (в т. М)
R (в т. М)
2) Определяем 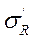 – в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
– в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
3) Определяем 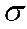 z;
z; 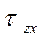 ;
; 
1 этап:
Пусть под действием силы Р точка М – переместилась в точку М1
S – перемещение т. М
можно записать
S =A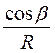 ; S1=A ; S1=A
|
  cos 0° = 1 Smax R= 0 cos 0° = 1 Smax R= 0
  cos 90° = 0 Smin R= cos 90° = 0 Smin R=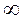 А – коэффициент пропорциональности
А – коэффициент пропорциональности
|
Относительное перемещение точки:



 еR =
еR = 
 =
=

Согласно 1 постулата теории упругости между напряжениями и деформациями должна быть прямая зависимость между Ϭ и ɛ, т.е.

 R = B еR =AB
R = B еR =AB В – коэффициент пропорциональности
В – коэффициент пропорциональности
 АВ?
АВ?
 R – определяется как в сопромате («метод сечений» мысленно
R – определяется как в сопромате («метод сечений» мысленно
разрезают балку и оставшуюся часть уравновешивают).
Р

 зз зз
 R R 
Z | Здесь поступаем также. Рассматриваем полушаровое сечение и заменяем отброшенное пространство напряжениями  Рассмотрим изменение
Рассмотрим изменение  в пределах в пределах  Составим уравнение равновесия на ось Z:
Составим уравнение равновесия на ось Z:
|
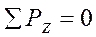




Отсюда  тогда
тогда  R =
R =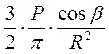
2 этап:
      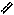 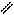 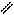 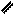 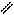 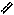    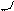  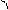         Р
Y Р
Y
 X X 
  R R
 М М
  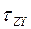 
 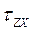 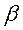 Z
Z
| Из геометрических соотношений:
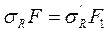 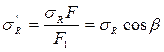
 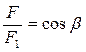  = =

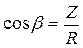  = =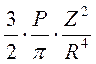
|
 3 этап:
3 этап:
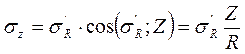 ;
; 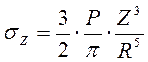
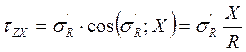 ;
; 

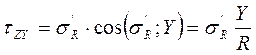 ;
; 
 Зная, что
Зная, что 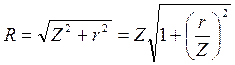 , подставим и получим
, подставим и получим
 ;
; 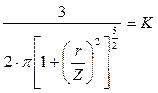 ;
;  ;
;  - опред. по таблице
- опред. по таблице  ;
; 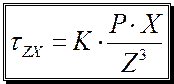
5.4 Определение напряжений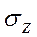 в массиве грунта от действия нескольких сосредоточенных сил.
в массиве грунта от действия нескольких сосредоточенных сил.
(принцип Сен-Венана – принцип независимости действия сил)
Р1 Р2 Р3
r2
| 

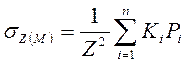 K=f K=f 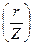
|
5.4 Определение напряжений  при действии любой распределённой нагрузки (метод элементарного суммирования)
при действии любой распределённой нагрузки (метод элементарного суммирования)
                       Pi Pi=qifi
Z R Pi Pi=qifi
Z R
 M r
элемент M r
элемент
 М r М r
| Задачу решаем приближённо. Разбиваем площадь на ряд простых многоугольников.Рассмотрим ri элемент
szi=Ki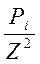 Pi – нагрузка на данный элемент
Pi – нагрузка на данный элемент
 szi =
szi =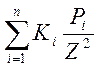
|
Ki=f 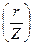 ; Эта задача трудоёмкая, особенно при большом числе элементов
; Эта задача трудоёмкая, особенно при большом числе элементов
 Достоинства:
1- способ универсален Достоинства:
1- способ универсален
| Недостатки: 1- точность зависит от табличных данных 2- значительная трудоемкость |
5.5 Определение  – под центром прямоугольной площадки
– под центром прямоугольной площадки
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1364; Нарушение авторских прав?; Мы поможем в написании вашей работы!



 S
S






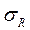 эп.
эп. 


 r3
r3