Закономерности в строении насаждении. Задаток – это передача денежных сумм в счет платежа по договору в доказательство его заключения

ЛЕКЦИЯ 7

Шестой способ

Задаток.

Задаток – это передача денежных сумм в счет платежа по договору в доказательство его заключения. Четыре функции задатка:

• Платежная.
• Удостоверительная. Например, продавец получает некоторые гарантии
• Обеспечительная. Например, не появится новый покупатель, в силу того, что вы уже внесли задаток
• Компенсационная.

Способы прекращения обязательств:

Прекращение обязательств – это разрыв юридической связи между кредитором и должником. Две группы:

1. Зависящие от воли
2. Не зависящие от воли

Первая группа:

• Надлежащее исполнение обязательств
• Отступление (ст. 459). Форма должна быть письменной

o Зачет (ст. 410 – ст. 412). В виде зачета можно отменить только требования однородные. Требования должны носить только встречный характер. Срок исполнения обязательств должен наступить. Для зачета необходимо заявления одной из сторон (односторонняя сделка).

o Новация. Это замена первоначального обязательства другим.

o Прощение долга. Ст. 415.

Вторая группа:

o Смерть кредитора или должника.

o Издание

Перечислительная таксация. Подерёвный, сплошной и частичный перечёты. Разделение по толщине и категориям. Перечётная ведомость. Закономерности распределения деревьев элемента леса по толщине в однородных древостоях. Положение среднего дерева. Ранги деревьев. Редукционные числа, естественные ступени толщины.

В любом древостое, состоящем из достаточно большого числа деревьев (не менее 150...200), можно проследить определенные закономерности в его строении. Четко проявляются распределения числа деревьев по их толщине, высоте, запасу и другим таксационным показателям. Эти закономерности наиболее четко проявляются в простых по форме, чистых по составу, одновозрастных и не тронутых рубками насаждениях или в древостоях одного элемента леса.

Из выявленных закономерностей наиболее важными являются следующие:

· распределение числа деревьев по толщине деревьев,

· распределение сумм площадей сечений и запасов по ступеням толщины;

· изменение высоты, видовых чисел и видовой высоты по ступеням толщины;

· взаимосвязь между отдельными таксационными показателями.

Ряд распределения числа деревьев по толщине является основным показателем, определяющим строение древостоя. Все основные таксационные показатели (средний диаметр, средняя высота и др.) зависят от него. Поясним это на примере.

Допустим, что в результате перечета было получено следующее распределение деревьев элемента леса по ступеням толщины:

Ступени толщины, см
Всего число деревьев, шт.
Число деревьев, %	1,6	4,6	10,4	19,4	22,0	20,4	11,8	6,2	2,8	0,8

Если нанести данные перечетной ведомости на график, отложив по горизонтали ступени толщины, а по вертикали - число деревьев (рис. 1), то можно заметить, что полученная кривая поднимается от тонких ступеней к средним, достигает максимума, а затем вновь снижается. Эта общая закономерность свидетельствует о том, что наибольшее число деревьев приходится на средние ступени толщины, а меньшее - на крайние (самые толстые и самые тонкие).

Рис. 1. Распределение числа деревьев по ступеням толщины.

Рис. 2. Накопленное распределение частот по естественным ступеням толщины (огива, кумулята)

В спелых, естественно-сформировавшихся нормальных насаждениях, состоящих из одного элемента леса, распределение деревьев по ступеням толщины характеризуется симметричной одновершинной кривой, называемой кривой нормального распределения. Для насаждений сложных, смешанных, разновозрастных или пройденных рубками, вид кривой меняется.

Например, для сложных разновозрастных древостоев, состоящих из нескольких пород и поколений, кривая может иметь две вершины или больше; в молодняках или насаждениях, пройденных рубками ухода по низовому методу, вершина кривой смещается вправо, в сторону толстых ступеней, а в древостое, пройденном выборочными рубками, влево, т. е. наблюдается асимметричное распределение, и т. д.

Исследованием строения насаждений занимались многие зарубежные и отечественные ученые. Еще в 1880 г. немецкий ученый В. Вейзе выявил, что среднее по толщине дерево древостоя занимает строго определенное место.

Оказалось, что число деревьев тоньше среднего диаметра составляет 57,5% от общего их числа, а толще 42,5%. Австрийский лесовод А. Шиффель (1903), при изучении распределение числа деревьев в процентном ряду от самого тонкого, до самого толстого ввёл понятие редукционного числа.

Редукционное число это отношение любого диаметра деревьев к среднему арифметическому значению.

Зная редукционные числа и средние значения таксационных показателей древостоя, можно найти значения этих показателей для любого дерева, занимающего разное положение в древостое без данных натурных измерений. Допустим, в еловом древостое со средним диаметром 40см требуется найти диаметр дерева, отстоящего от самого тонкого на 30 %.

Тогда d₃₀=D_ср*R_d=40*0,84=33,6 см, где R_d - редукционное число по Шиффелю, равное 0,84.

Из отечественных ученых наибольший вклад в изучение закономерностей строения насаждений внесли А. В. Тюрин и Н. В. Третьяков.

Чтобы привести различные ряды распределения к сопоставимому виду, А. В. Тюрин перешел от абсолютных ступеней толщины в сантиметрах к относительным, выраженным в десятых долях от среднего диаметра, т. е. к редукционным числам по диаметру Rd.

А. В. Тюрин назвал их естественными ступенями толщины. Принимая значение таксационного при знака среднего дерева насаждения за единицу, он проследил изменения по естественным ступеням не только диаметров, но и других таксационных признаков древостоев. Он выявил, что процентное распределение деревьев по естественным ступеням толщины не зависит от породы, класса бонитета и полноты, а лишь в некоторой степени зависит от возраста и большей мере - от характера рубок ухода.

По данным А. В. Тюрина и других авторов (Н. П. Анучина, Н. В. Третьякова и др.) получены следующие выводы:

1. Если средний диаметр древостоя Dср принять за 1,0, то редукционное число Rd самых тонких его деревьев равно половине среднего диаметра 0,5 Dcр (по другим данным 0,4 Dср), а самых толстых — 1,7 Dср (в молодняках 2...2,5 Dср), т. е. самое толстое дерево в древостое примерно в 4 раза толще самого тонкого. Таким образом, все число стволов, по данным А. В. Тюрина, укладывается в рамки 13 естественных ступеней толщины.

2. Если последовательно суммировать число стволов по естественным ступеням толщины, начиная с самой малой (тонкой), и по полученным данным построить график, то получим кривую, которая в статистике называется огивой (рис. 2). Такие же графики могут быть построены и по суммам площадей сечений и запасам.

Располагая такими графиками, можно показать зависимость между диаметром деревьев и их местом (рангом) в насаждении по числу стволов, сумме площадей сечений и запасам. Так, суммарное число стволов в ступенях меньше среднего по диаметру дерева (естественная ступень 1,0) равно 57...58%, или, иначе, среднее (по диаметру) дерево находится на 58-м месте по проценту числа стволов, начиная с самой малой ступени.

Эта закономерность может быть использована для определения среднего диаметра нормальных насаждений непосредственно по перечетной ведомости. Для этого достаточно суммировать проценты числа стволов по направлению от малых ступеней к большим (толстым), пока не наберется 58% (округленно 60 %).

3. Дерево, имеющее средний диаметр, имеет и среднюю высоту, среднюю площадь сечения, средний объем и т. д., или, иначе, среднее по диаметру дерево в древостое является также средним и по остальным таксационным показателям. Эта связь используется для определения средних таксационных показателей древостоя (метод средней модели).

4. Редукционные числа по площади сечения и по объему так же, как их ряды распределения и огивы, очень близки. Так, самые тонкие деревья древостоя по площади сечения составляют 0,25, а по объему 0,22 от среднего дерева, а самые толстые по обоим показателям 2,89. Это значит, что объем тонкого дерева составляет всего 22% от объема среднего дерева, а объем самого толстого больше среднего в 2,9 раза. Площадь сечения и объем самого тонкого дерева в насаждении в 12 раз меньше, чем самого толстого. Близость редукционных чисел по площади сечения и объему свидетельствует о том, что между ними имеется очень тесная прямолинейная зависимость, она характеризуется коэффициентами корреляции 0,92...0,98.

5. Между диаметром и высотой по естественным ступеням толщины наблюдаются определенные соотношения. Если среднюю высоту насаждения принять за 1,0, то пределы высоты будут: минимальный 0,80, максимальный 1,15; в молодых насаждениях эти пределы несколько больше, а в старых меньше. Связь высоты с диаметром довольно тесная и характеризуется высоким корреляционным отношением, равным 0,95 и выше.

6. Относительный сбег и полнодревесность стволов, характеризуемые коэффициентами формы и видовыми числами, уменьшаются от низших ступеней толщины к высшим. Изменение видовых чисел по естественным ступеням толщины выражается линейным уравнением.

Изложенные основные закономерности строения насаждений имеют большое теоретическое и практическое значение. В частности, А. В. Тюрин на основании полученных им данных составил специальные таблицы распределения числа деревьев для насаждений с различными средними диаметрами (табл. 2 (3.8)).

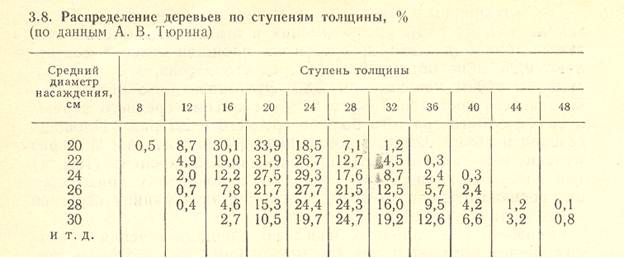
Аналогичные таблицы составлены по суммам площадей сечений и запасам. По ним, не имея данных перечета, а зная лишь средний диаметр древостоя, можно распределить общий запас по отдельным ступеням толщины. Подобные таблицы служат также основой для составления товарных таблиц, в которых приведено распределение запаса по сортиментам.

Н. В. Третьяков выявил, что закономерности строения древостоя для нормальных насаждений, свойственны каждому элементу леса смешанных и сложных насаждений. Приведенные выше закономерности позволяют судить о границах изменения и средних значениях отдельных таксационных показателей всего насаждения и его отдельных частей. Они облегчают познание природы леса и служат основой для разработки более рациональных методов его учета. Однако при изучении закономерностей строения насаждений надо иметь в виду, что они носят статистический характер и выявляются только в насаждениях с достаточным числом деревьев. Возводить эти закономерности в абсолютный закон не следует. Попытка произвести подобные расчеты на ограниченном материале может привести к значительным отклонениям от приведенных рядов распределения.

Дата добавления: 2014-01-20