
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория винтовой пары
|
|
|
|
Зависимость между моментом, приложенным к гайке и осевой силой винта. Если винт нагружен осевой силой  (рис. 1.13), то для завинчивания гайки к ключу необходимо приложить момент
(рис. 1.13), то для завинчивания гайки к ключу необходимо приложить момент 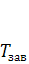 , а к стержню винта – реактивный момент
, а к стержню винта – реактивный момент  , который удерживает стержень от вращения. При этом можно записать
, который удерживает стержень от вращения. При этом можно записать
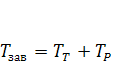 (1.3)
(1.3)
где  – момент сил трения на опорном торце гайки;
– момент сил трения на опорном торце гайки;  – момент сил трения в резьбе. Равенство (1.3), так же как и последующие зависимости, справедливо для любых винтовых пар болтов, винтов, шпилек и винтовых механизмов.
– момент сил трения в резьбе. Равенство (1.3), так же как и последующие зависимости, справедливо для любых винтовых пар болтов, винтов, шпилек и винтовых механизмов.
Не допуская существенной погрешности, принимают приведенный радиус сил трения на опорном торце гайки равным среднему радиусу этого торца или 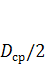 . При этом
. При этом
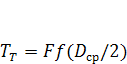 , (1.4)
, (1.4)
где 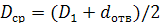 ;
; 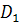 – наружный диаметр опорного торца гайки;
– наружный диаметр опорного торца гайки; 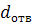 – диаметр отверстия под винт;
– диаметр отверстия под винт; 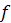 – коэффициент трения на торце гайки.
– коэффициент трения на торце гайки.
Момент сил трения в резьбе определим, рассматривая гайку как ползун, поднимающийся по виткам резьбы, как по наклонной плоскости (рис. 1.14, а). По известной теореме механики, учитывающей силы трения, ползун находится в равновесии, если равнодействующая 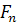 системы внешних сил отклонена от нормали п – п на угол трения
системы внешних сил отклонена от нормали п – п на угол трения 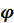 . В нашем случае внешними являются осевая сила
. В нашем случае внешними являются осевая сила 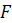 и окружная сила
и окружная сила 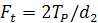 . Здесь
. Здесь 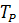 – не реактивный, а активный момент со стороны ключа, равный
– не реактивный, а активный момент со стороны ключа, равный 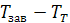 [см. формулу (1.3)].
[см. формулу (1.3)].
Далее (рис. 1.14), 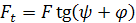 или
или
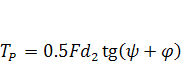 , (1.5)
, (1.5)
где 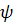 – угол подъема резьбы [по формуле (1.1)];
– угол подъема резьбы [по формуле (1.1)];  – угол трения в резьбе;
– угол трения в резьбе; 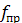 – приведенный коэффициент трения в резьбе, учитывающий влияние угла профиля [формула (1.2)].
– приведенный коэффициент трения в резьбе, учитывающий влияние угла профиля [формула (1.2)].
Подставляя значения моментов в формулу (1.3), найдем искомую зависимость:
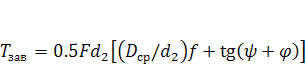 . (1.6)
. (1.6)
При отвинчивании гайки окружная сила 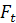 , и силы трения меняют направление (рис. 1.14, б). При этом получим
, и силы трения меняют направление (рис. 1.14, б). При этом получим
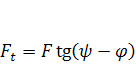 . (1.7)
. (1.7)
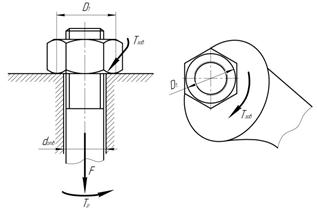
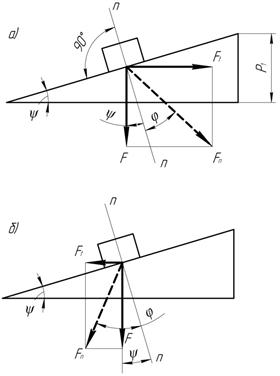
Рис. 1.13 Рис. 1.14
Момент отвинчивания с учетом трения на торце гайки, по аналогии с формулой (1.6),
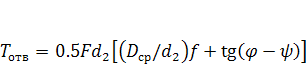 . (1.8)
. (1.8)
Полученные зависимости позволяют отметить:
1. По формуле (1.6) можно подсчитать отношение осевой силы винта 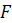 к силе
к силе 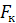 , приложенной на ручке ключа, т. е.
, приложенной на ручке ключа, т. е. 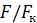 , которое дает выигрыш в силе. Для стандартных метрических резьб при стандартной длине ключа
, которое дает выигрыш в силе. Для стандартных метрических резьб при стандартной длине ключа 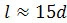 и
и 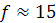
 (см. табл. 1.6).
(см. табл. 1.6).
2. Стержень винта не только растягивается силой 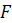 , но и закручивается моментом
, но и закручивается моментом 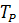 .
.
Самоторможение и КПД винтовой пары. Условие самоторможения можно записать в виде 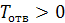 , где
, где 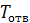 определяется по формуле (1.8). Рассматривая самоторможение только в резьбе без учета трения на торце гайки, получим
определяется по формуле (1.8). Рассматривая самоторможение только в резьбе без учета трения на торце гайки, получим 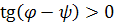 или
или
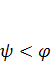 . (1.9)
. (1.9)
Для крепежных резьб значение угла подъема 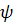 лежит в пределах
лежит в пределах  , а угол трения
, а угол трения 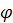 изменяется в зависимости от коэффициента трения в пределах от
изменяется в зависимости от коэффициента трения в пределах от  (при
(при 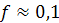 ) до
) до 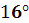 (при
(при 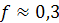 ). Таким образом, все крепежные резьбы – самотормозящие. Ходовые резьбы выполняют как самотормозящими, так и несамотормозящими.
). Таким образом, все крепежные резьбы – самотормозящие. Ходовые резьбы выполняют как самотормозящими, так и несамотормозящими.
Приведенные выше значения коэффициента трения, свидетельствующие о значительных запасах самоторможения, справедливы только при статических нагрузках. При переменных нагрузках и особенно при вибрациях вследствие взаимных микросмещений поверхностей трения (например, в результате радиальных упругих деформаций гайки и стержня винта) коэффициент трения существенно снижается (до 0,02 и ниже). Условие самоторможения нарушается. Происходит самоотвинчивание.
КПД  винтовой пары представляет интерес главным образом для винтовых механизмов. Его можно вычислить по отношению работы, затраченной на завинчивание гайки без учета трения к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отношение работ равно отношению моментов
винтовой пары представляет интерес главным образом для винтовых механизмов. Его можно вычислить по отношению работы, затраченной на завинчивание гайки без учета трения к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отношение работ равно отношению моментов 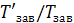 , в котором
, в котором 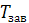 определяется по формуле (1.6), а
определяется по формуле (1.6), а 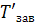 – по той же формуле, но при
– по той же формуле, но при 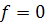 и
и 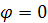 :
:
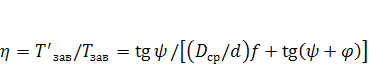 . (1.10)
. (1.10)
Учитывая потери только в резьбе ( = 0), найдем КПД собственно винтовой пары:
= 0), найдем КПД собственно винтовой пары:
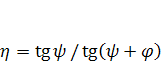 . (1.11)
. (1.11)
В самотормозящей паре, где 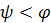 ,
, 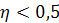 . Так как большинство винтовых механизмов самотормозящие, то их КПД меньше 0,5.
. Так как большинство винтовых механизмов самотормозящие, то их КПД меньше 0,5.
Формула (1.11) позволяет отметить, что  возрастает с увеличением
возрастает с увеличением 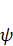 и уменьшением
и уменьшением  .
.
Для увеличения угла подъема резьбы 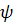 в винтовых механизмах применяют многозаходные винты. В практике редко используют винты, у которых
в винтовых механизмах применяют многозаходные винты. В практике редко используют винты, у которых 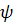 больше
больше 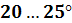 , так как дальнейший прирост КПД незначителен, а изготовление резьбы затруднено. Кроме того, при большем значении
, так как дальнейший прирост КПД незначителен, а изготовление резьбы затруднено. Кроме того, при большем значении 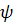 становится малым выигрыш в силе или передаточное отношение винтовой пары (см. гл. 14).
становится малым выигрыш в силе или передаточное отношение винтовой пары (см. гл. 14).
Для повышения КПД винтовых механизмов используют также различные средства, понижающие трение в резьбе: антифрикционные металлы, тщательную обработку и смазку трущихся поверхностей, установку подшипников под гайку или упорный торец винта, применение шариковых винтовых пар и пр.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2492; Нарушение авторских прав?; Мы поможем в написании вашей работы!