Балансировка бинарного дерева поиска

План

Интерактивный генератор отчетов

Пакет деловой графики

Многофункциональный текстовый процессор

Предназначен для просмотра и редактирования текстов, обработки больших массивов данных.

Основные возможности программы:

1. одновременное редактирование нескольких файлов в разных окнах;

2. поддержка строковых и матричных блоков;

3. сортировка блоков и вычисления в блоке;

4. поиск текста и замена, преобразование строчных и заглавных букв;

5. поддержка стилей, табличный режим редактирования;

6. форматирование текста, режим автореформатирования;

7. встроенный калькулятор;

8. функция поиска файлов;

9. поддержка различных моделей принтеров.

Предназначен для создания графических отчетов по данным, извлекаемым из таблиц БД или подготовленным любым другим образом.

Возможности пакета:

1. создание диаграмм;

2. эффект трехмерности при изображении диаграмм;

3. вывод легенды;

4. гибкое задание данных (матрицей, по столбцам, по строкам);

5. синхронизация независимых блоков данных по легендам;

6. возврат к ранее заданным сериям данных;

7. несколько графиков на одной странице (экране) с размещением в координатах виртуального экрана;

8. несколько серий на одном графике;

9. многостраничные отчеты;

10. генерация многостраничных отчетов по заданному числу серий на одной странице;

11. сортировка данных перед построением;

12. вывод на график линий минимума, максимума и среднего значения;

13. использование шрифтов, линий и фона разных стилей, цветов и размеров;

14. отбор заданного числа первых точек с возможностью суммирования отброшенных (в том числе по модулю);

15. возможность выводить изображение в черно-белом режиме, с использованием чистых цветов и цветных штриховок;

16. печать графических отчетов на принтере;

17. вывод графических отчетов в файл формата PCX.

Предназначен для интерактивного формирования сложных отчетов по любым данным, извлекаемым из БД.

Возможности программы:

1. создание и модификация отчетов;

2. вставка в отчет полей Базы Данных, вычисляемых полей, специальных функций;

3. расчет сумм, максимумов, минимумов, средних значений;

4. вложенные циклы, заголовки и подножия;

5. стили, форматирование данных, перенос по словам, разбиение на страницы;

6. формирование параметрических фильтров для селективного выбора данных при выполнении отчета;

7. объединение однотипных отчетов в группы;

8. сохранение отчетов в библиотеку для последующего быстрого вызова.

1. Балансировка бинарного дерева поиска

2. Упорядочивание массива методом вставки

3. Функция, упорядочивающая массив

Алгоритмы вставки элемента в бинарное дерево поиска, поиска элемента по ключу, удаления элемента из бинарного дерева поиска требуют количества операций линейно зависящее от высоты дерева .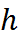

При вставке элементов в бинарное дерево поиска дерево может иметь как вид а) так и вид б).

а) б)

Очевидно, что в случае а) высота дерева равна числу узлов. Поэтому возникает задача приведения бинарного дерева поиска к виду с высотой как можно меньше.

Введём понятие уровня узла А.

Если узел А является корнем дерева Т, он принадлежит первому уровню.

В противном случае уровень узла на единицу больше чем уровень его предка.

Бинарное дерево Т, имеющее высоту 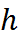, является совершенным, если выполняются следующие условия:

1. все узлы, начиная с уровня и выше, имеют по два дочерних узла;

2.если узел, находящийся на уровне , имеет дочерние узлы, то все узлы, находящиеся на этом же уровне слева от него, имеют по два дочерних узла;

3.если узел, находящийся на уровне , имеет один дочерний узел, то он является его левым дочерним узлом.

При симметричном обходе бинарного дерева поиска узлы посещаются в порядке возрастания ключа.

Если есть достаточное количество памяти, то можно воспользоваться следующим методом приведения бинарного дерева поиска к дереву с минимальной высотой.

Записать все элементы из бинарного дерева поиска в массив при симметричном обходе, при этом массив будет упорядочен по возрастанию ключа.

Удалить исходное дерево.

Создать пустое бинарное дерево поиска.

Вставлять элементы из массива длины при помощи следующей рекурсивной функции (псевдокод).

Insert_from_array(BinaryTree *binTree, Type_elem *a, int n)

{

if(n == 0) return;

else{

Insert(binTree, a[n/2]);

Insert_from_array(binTree, a, (n/2));

Insert_from_array(binTree, &a[n/2+1],(n-(n/2)-1));

}

}

Здесь Insert(BinaryTree *binTree, Type_elem a) – функция вставляющая элемент в бинарное дерево поиска.

			…		…
			…		…

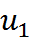
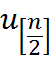
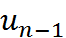
Для действительного числа обозначим 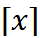– верхнюю грань, т.е. минимальное число не меньшее . Для дерева T обозначим его высоту. Докажем, что построенное таким образом бинарное дерево, с числом вершин , имеет высоту равную .

Доказательство по индукции.

1. При , 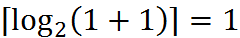утверждение верно.

2.Предположим, что оно верно при всех .

3.Докажем для 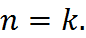Высота полученного дерева равна 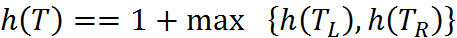. Поскольку левое поддерево содержит не меньше вершин, чем правое, то

Утверждение доказано.

В случае, когда нет возможности приводить дерево к дереву с минимальной высотой, приводят дерево к виду с высотой близкой к минимальной.

Бинарное дерево поиска называется сбалансированным по высоте, или просто сбалансированным, если высота правого поддерева любого его узла отличается от высоты левого поддерева не больше чем на 1.

Сбалансированное бинарное дерево поиска с узлами имеет высоту между 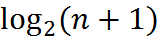и 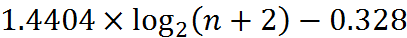(см. D. Knuth, The Art of Computer Programming, v.3).

Методы балансировки бинарных деревьев, требующие существенно меньших затрат памяти, чем изложенный, не рассматриваются в данном курсе.

Дата добавления: 2014-01-20