Параметрические уравнения

Как уже было сказано выше, кривые можно представлять аналитически и графически, т. е. как график функции. Математики записывают это следующим образом:

y=f(x)

что означает "значение у — это функция, т. е. зависимость, от значения х", например простейшая функция у = 2х означает простейшую зависимость: каждое значение у в два раза больше любого значения х. График этой функции представляет собой прямую линию, проходящую через начало координат (рис. 12.2).

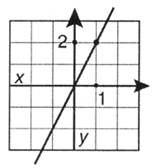
Рис. 12.2. График функции у = 2х

Более интересный вид представляют собой тригонометрические функции, например синусоида:

у = sin х. График такой кривой известен каждому (рис. 12.3).

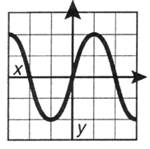
Рис. 12.3. График функции у = sin x

Такой способ представления формулы и ее графика называется явным. Он позволяет относительно легко строить график. Однако у этого способа с точки зрения графического представления имеются весьма существенные недостатки.

Каждому значению х соответствует только одно значение у. Это не дает возможности начинать новый фрагмент кривой в произвольном месте.

Кривая не может быть замкнутой.

В результате явный способ представления не может применяться там, где требуется описание произвольных кривых, размещаемых в произвольных местах на плоскости.

Альтернативным способом является определение кривой как параметрической функции.

В первую очередь очень важно отметить следующую особенность: у такого способа обе координаты (х и у) являются равноправными, т. е. вычисляются как функции некоего вспомогательного параметра, обозначаемого, как правило, символом t. В общем случае такая зависимость получает вид:

q(t) = {x(t), y(t)},

где х(t) и y(t) — функции параметра t.

Задавая одинаковые значения t, функция x(t) вычисляет значения координаты х, а функция y(t) — значения координаты у.

Дата добавления: 2014-01-20