Системы с одной степенью свободы при отсутствии трения

Силовое возбуждение колебаний

Независимо от природы вынуждающих сил будем исходить из того, что каждая из них задана в виде некоторой функции времени 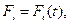где 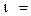1,2,...,n - порядковый номер материальной точки.

Рассмотрим простейшую систему с одной степенью свободы, которая совершает колебания под действием вынуждающей силы F(t). В любой момент времени на груз массой m действуют две силы: сила упругости пружины, пропорциональная смещению груза X, и возмущающая сила F(t), изменяющаяся во времени по некоторому, заранее заданному закону.

Дифференциальное уравнение движения груза:

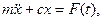
где С - жесткость пружины,

или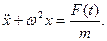

Это уравнение иногда называют стандартным, так как к нему можно прийти и при рассмотрении других систем с одной степенью свободы, имеющих совершенно иной конструктивный вид.

Действие гармонической силы

Случай, когда возмущающая сила изменяется по гармоническому закону

F=F₀ sin pt,

где F₀ - амплитуда силы; p - её частота, является наиболее распространённым в практике.

Поскольку дифференциальное уравнение движения в данном случае получилось неоднородным, то его решение складывается из общего решения однородного уравнения, которое мы уже получили, и частного решения неоднородного, т.е. любого решения, удовлетворяющего дифференциальному уравнению. Это решение будем искать в форме правой части, т.е.

,

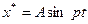где А – амплитуда вынужденных колебаний. После подстановки в дифференциальное уравнение, находим

,

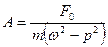следовательно,

Следовательно, при произвольных начальных условиях возникают сложные колебания, состоящие из двух частей: колебаний, происходящих с частотой p возмущающей силы, и колебаний, происходящих с собственной частотой 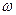. Обычно первые колебания называют вынужденными, а вторые - свободными. Такая терминология является условной. Дело в том, что и вторые колебания вызваны действующей возмущающей силой, и их амплитуда зависит от этой силы; в этом смысле вторые колебания также являются вынужденными. Указанные наименования получили широкое распространение потому, что первое слагаемое имеет частоту возмущающей силы, а второе меняется с собственной частотой системы.

Составляющая, названная выше свободными колебаниями, быстро исчезает, поэтому достаточно ограничиться изучением стационарной, незатухающей части решения

.

Амплитуда вынужденных колебаний

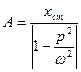
отличается от прогиба 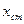, подсчитанного в предположении статического действия силы F₀. Отношение 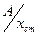можно назвать динамическим коэффициентом

.

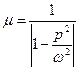Динамический коэффициент 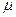зависит только от отношения частот .

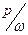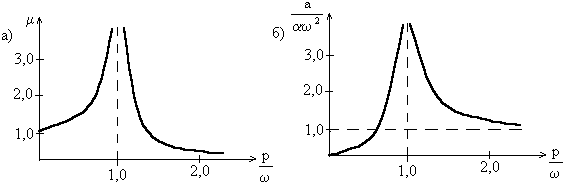
При малой частоте возмущающей силы динамический коэффициент близок к единице. С ростом частоты p динамический коэффициент быстро увеличивается и при 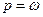обращается в бесконечность. Это соответствует состоянию резонанса, когда амплитуда вынужденных колебаний стремится к бесконечности (если учесть силы неупругого сопротивления, то амплитуда при резонансе окажется хотя и ограниченной, но обычно настолько значительной, что состояние резонанса всё равно следует считать опасным).

Если частота p больше собственной частоты 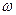, то амплитуды становятся конечными; при 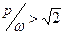динамический коэффициент становится меньше единицы, т.е. динамический эффект слабее соответствующего статического эффекта. При очень больших значениях отношения 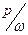динамический коэффициент становится весьма малым. Это означает, что сила высокой частоты не вызывает ощутимых колебаний в упругой низкочастотной системе, которая как бы "не успевает" отзываться на быстрые изменения возмущающей силы.

Механическая система. Силы внешние и внутренние

Дата добавления: 2014-01-20