Кривые линии и поверхности

Кривую линию можно рассматривать:

• как траекторию движения точки на плоскости или в пространстве,

• а также как совокупность точек, удовлетворяющих определенному уравнению.

Кривая линия определяется положением составляющих ее

точек. Точки кривой определяются ее координатами.

Кривую линию называют плоской,

если все точки линии лежат в одной плоскости, и пространственной,

если точки не принадлежат одной плоскости.

Примеры плоских кривых линий:

• окружность,

• парабола,

• эллипс,

• гипербола и т.д.

Примеры пространственной кривой линии: винтовая линия.

Рис. 3.1

Для построения проекций кривых линий строят проекции ряда принадлежащих ей точек.

Пространственная кривая проецируется в виде плоской, плоская кривая – также в виде плоской или в виде прямой линии, если кривая находится в проецирующей плоскости.

Большой интерес представляет проекция окружности.

Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров. Удобнее всего строить проекции диаметров, параллельных плоскостям проекции.

• Построить три проекции окружности радиусом 20 мм, параллельной плоскости П 2.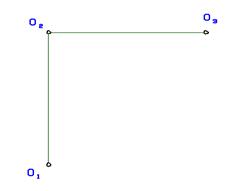

Рис. 3.2

• Так как окружность параллельна фронтальной плоскости проекций, то на эту плоскость она будет проецироваться в натуральную величину.

Так как окружность расположена во фронтальной плоскости уровня, то на горизонтальную плоскость проекций П ₁ она будет проецироваться в виде отрезка, равного диаметру окружности d.

• На профильную плоскость проекций П ₃

окружность также будет проецироваться в виде отрезка, равного диаметру окружности d.

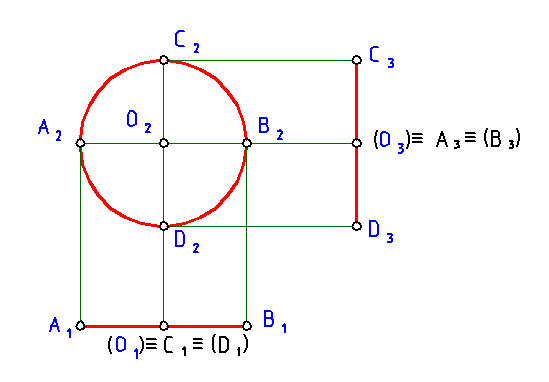
Рис. 3.3

Если окружность расположена в проецирующей плоскости, то на плоскость, ей перпендикулярную, она проецируется в виде отрезка прямой, равного диаметру окружности, а на две другие – в виде эллипса.

Большая ось эллипса всегда равна диаметру окружности.

Малая ось эллипса зависит от угла наклона плоскости окружности к соответствующей плоскости проекций.

2 a = d

2b = d * Cos α

Задача 12

Построить три проекции окружности диаметром 40 мм, принадлежащей плоскости Σ (Σ ₂).

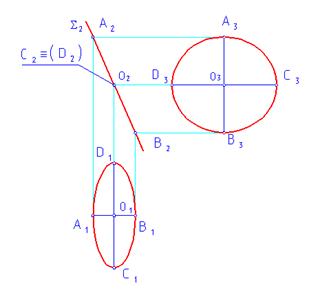
Рис. 3.4

Задание поверхности на комплексном чертеже

Для задания поверхности могут быть использованы три основных способа:

• Аналитический

• Каркасный

• Кинематический

При аналитическом способе задания поверхность рассматривается как множество точек, координаты которых удовлетворяют заданному уравнению. В этом случае поверхность задается уравнением.

• При каркасном способе задания поверхность рассматривается как совокупность достаточно плотной сети линий, определяющих поверхность.

• Эта сеть называется каркасом.

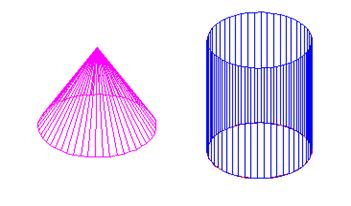
Рис. 3.5 Рис. 3.6

При кинематическом способе задания поверхность рассматривается как совокупность всех положений движущейся линии.

Этот способ задания поверхности является предпочтительным в инженерной графике.

• Закон перемещения образующей обычно определяется другими линиями, по которым перемещается образующая при своем движении.

• Эта линия называется направляющей m.

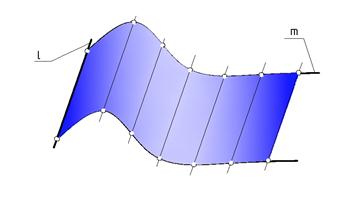
Рис. 3.7

В этом случае поверхность задается ее определителем ( совокупность геометрических элементов, определяющих поверхность).

Определитель состоит из графической и алгоритмической части.

• Определитель вполне задает поверхность на чертеже.

• В общем случае поверхность считается заданной, если относительно любой точки пространства можно ответить на вопрос:

• принадлежит или нет данная точка поверхности.

Поверхность задана определителем

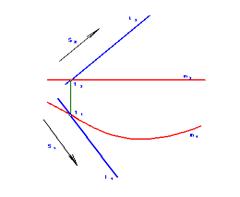
Рис. 3.8

Гранные поверхности

• Поверхности, образованные перемещением прямолинейной образующей по ломаной линии, называются гранными.

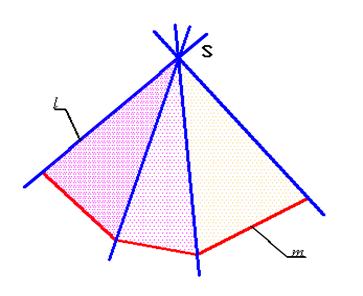
Рис. 3.9

Дата добавления: 2014-01-20