
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорія дискового відцентрового розкидача
|
|
|
|
Робочий процес відцентрового висіваючого апарату складається з 2 фаз: відносне переміщення частинок добрив по диску і падіння туків кинутих диском у горизонтальній площині.
Для визначення мінімальної необхідної частоти обертання диска, при якій спостерігається рух частинки по диску, розглянемо плоский диск із розташованою на ньому частинкою туків.
На частинку діють: сила тертя 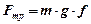 та відцентрова сила переносного руху
та відцентрова сила переносного руху 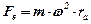 (рис. 7.3, а), а умова рівноваги частинки матиме вигляд
(рис. 7.3, а), а умова рівноваги частинки матиме вигляд
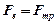 .
.
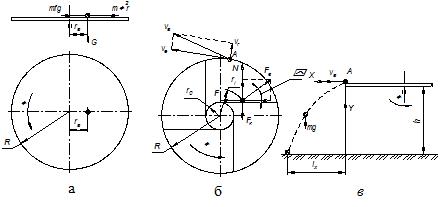
Рис. 7.3. Схема до розрахунку параметрів дискового відцентрового розкидаючого апарату
Або
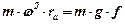 .
.
Якщо рахувати, що 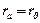 - мінімальному радіусу падіння туків із кузова, а
- мінімальному радіусу падіння туків із кузова, а 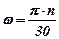 , то отримаємо
, то отримаємо
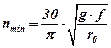 .
.
Таким чином, за частоти обертання розкидаючого диска 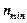 розрахованою за формулою (7.16) ще можливий рух частинки добрив по ньому.
розрахованою за формулою (7.16) ще можливий рух частинки добрив по ньому.
Частинка, яка впала на диск, через певний проміжок часу зустрінеться із лопаткою і далі продовжить свій рух вздовж неї. При цьому на частику добрив діють: відцентрова сила інерції  , яку можна розкласти на складову направлену вздовж лопатки
, яку можна розкласти на складову направлену вздовж лопатки 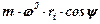 та перпендикулярно до неї
та перпендикулярно до неї 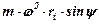 ; коріолісова сила інерції
; коріолісова сила інерції 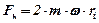 , яка діє у напрямку протилежному до напрямку коріолісового прискорення; сили тертя по диску
, яка діє у напрямку протилежному до напрямку коріолісового прискорення; сили тертя по диску 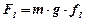 та по лопатці
та по лопатці 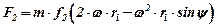 . Тоді умова рівноваги матиме вигляд
. Тоді умова рівноваги матиме вигляд
 .
.
Або
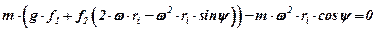 .
.
Якщо врахувати, що при граничних умовах 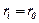 та
та 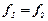 , то отримаємо
, то отримаємо
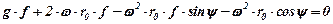 .
.
Звідки отримаємо
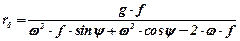 .
.
Таким повинен бути мінімальний радіус падіння частинок туків, для забезпечення їх руху вздовж лопатки.
Після досягнення частинкою краю лопатки відбувається її кидок та вільний політ. У цей момент абсолютна швидкість частики становить
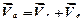 .
.
Але оскільки  , то можна прийняти, що
, то можна прийняти, що 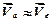 , тобто швидкості переносного руху частинки із диском.
, тобто швидкості переносного руху частинки із диском.
Без урахування опору повітря політ частинки може бути описаний системою
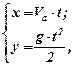
де 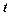 - час польоту частинки.
- час польоту частинки.
Із другого рівняння системи маємо при 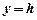
 ,
,
де 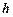 - висота встановлення розкидальних дисків над поверхнею поля, м
- висота встановлення розкидальних дисків над поверхнею поля, м
З урахуванням отриманого 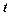 із першого рівняння системи (7.21) отримаємо
із першого рівняння системи (7.21) отримаємо
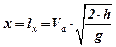 ,
,
де 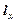 - віддаль польоту частинки, м.
- віддаль польоту частинки, м.
Використовуючи отриманий вираз можна записати залежність для визначення ширини захвату дводискового апарату
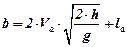 ,
,
де 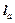 - віддаль між центрами дисків,
- віддаль між центрами дисків, 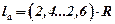 .
.
В існуючих машинах 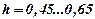 м;
м; 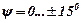 ;
; 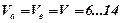 м/с;
м/с; 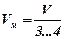 , де
, де 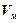 - поступальна швидкість машини.
- поступальна швидкість машини.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!