Предварительные факты

End

Begin

r:= b;

q:= 0;

While r >= b do begin

r:= r - a;

q:= q + 1

{Invariance equality: a = b*q + r, Invariant:a- b*q - r}

end;

Таким чином, поліноміальні інваріантні рівності мають вигляд 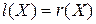, де 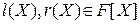. Інваріант, що відповідає цій рівності, має вигляд .

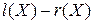Ідеали програмних інваріантів. Основні властивості.

Наведемо необхідні алгебраїчні визначення й твердження.

Множина називається ідеалом кільця 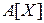, якщо

a) для будь-яких елементів 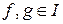різниця ;

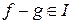b) для будь-яких елементів 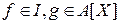добуток .

Базисом ідеалу 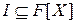називається скінчена система поліномів 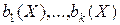кільця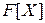така, що будь-який поліном 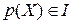може бути представлений у вигляді

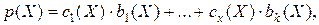де .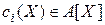

Теорема Гильберта про базис ідеалу комутативного кільця поліномів стверджує, що будь-який ідеал 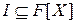має скінчений базис. Якщо 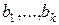- базис ідеалу 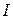, цей факт записують у вигляді 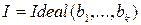або .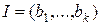

Нехай 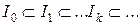- зростаюча послідовність ідеалів кільця 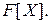Тоді ця послідовність є скінченою. Цю властивість називають властивістю нетеровості кільця 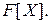Теорема Гильберта про базис і властивість нетеровості кільця 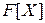- еквівалентні твердження. Кільця, що задовольняють цій властивості, називають нетеровими.

Ідеал називається простим, якщо із 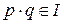слідує 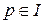або .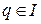

Ідеал називається радикальним, якщо із 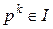слідує .

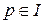Радикальний ідеал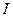можна представити у вигляді перетину скінченого числа простих ідеалів: .

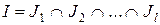Нехай 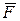- алгебраїчне замикання поля 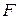. Многовидом (variety) ідеалу 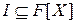називають множину 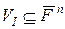таку, що .

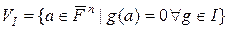Нехай 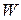-довільна підмножина . Тоді множина

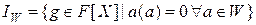
утворює ідеал кільця .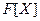

Якщо за ідеалом 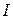побудувати 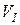, а потім розглянути ідеал 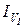, легко показати, що 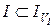. Якщо 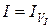, ідеал 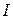називається ідеалом свого многовиду. Можна показати, що клас радикальних ідеалів співпадає з класом ідеалів своїх многовидів.

Множина поліноміальних інваріантів програми 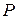є ідеалом свого многовиду, і отже - радикальним ідеалом кільця 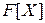, який ми будемо позначати через .

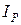Базиси ідеалів не володіють властивістю одиничності. Для того, щоб набути цю властивість, треба використати базиси Гребнера ідеалів (Комп’ютерна алгебра).

1. Множество инвариантов в произвольной контрольной точке императивной программы образует полиномиальный идеал над конструктивным полем.

2. Если в условиях операторов программы используются предикаты равенства и их отрицания, проблема построения базиса этого идеала алгоритмически неразрешима. Поэтому условия в операторах программы приходится игнорировать, считая вычисления абсолютно недетерминированными.

3. Для решения задач автоматической генерации программных инвариантов предлагаются итерационные методы статического анализа, называемые методами нижней и верхней аппроксимации.

,

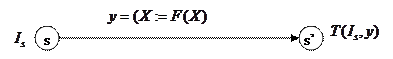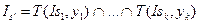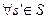
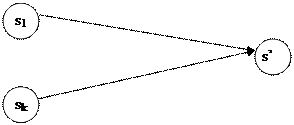
Система уравнений потокового анализа программ

,

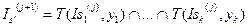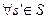
Итерационные соотношения потокового анализа программ

Метод нижней итерации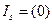

Метод верхней итерации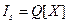

В нашей предметной области эти методы не дают полного решения – в виде базиса идеала инвариантов.

3. Предлагпается другой метод. Основные теоремы метода:

- теорема об алгоритмической разрешимости проблем доказательства инвариантности полиномиального равенства

- теорема об алгоритмической разрешимости проблемы построения базиса векторного пространства полиномиальных инвариантов ограниченной степени.

4. На основании этих теорем предложены алгоритмы решения указанных проблем с использованием техники базисов Гребнера.

Дата добавления: 2014-01-20