Критический путь и его анализ

После того как проведена идентификация операций, можно оценить их продолжительность. На основе продолжительности выполнения каждой операции и руководствуясь логической схемой, можно найти время выполнения проекта в целом. На данном этапе предполагается, что продолжительность выполнения каждой операции является фиксированной величиной, не испытывающей влияния неопределенности.

В каждом графе существует несколько возможных путей. Общее время, необходимое для того, чтобы пройти какой-либо путь, есть сумма выполнения всех операций, принадлежащих данному пути. Продолжительность выполнения всего проекта занимает наибольшее время. Более длительные операции называются критическими.

Критический путь - максимальный по продолжительности полный путь в сети (в сетевой модели) называется критическим; работы, лежащие на этом пути, называются критическими работами. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом. Как правило, критические работы составляют небольшую часть всех работ сети, но именно они определяют продолжительность выполнения комплекса в целом. Длительность выполнения всего проекта в целом может быть сокращена за счет сокращения длительности задач, лежащих на критическом пути. Соответственно, любая задержка выполнения задач критического пути повлечет увеличение длительности проекта.

Существуют также работы с очень маленькими резервами времени. Они являются субкритическими и на них нужно обращать столько же внимания, сколько и на критические работы.

В каждом графе найдется по крайней мере один критический путь. Для того, чтобы найти общую продолжительность выполнения проекта, нужно определить продолжительность критического пути. В большинстве графов идентифицировать все идущие сквозь граф пути, чтобы выявить среди них тот, который занимает наибольшее время, достаточно трудно.

Метод критического пути (КМП) - является основным математическим средством для вычисления ранних и поздних начал и окончаний работ и резервов времени.

Существует два возможных метода, позволяющих отследить движение времени в графе:

1. Определение для каждой операции наиболее ранних сроков начала и окончания ее выполнения.

2. Определение для каждого события наиболее раннего срока его наступления.

Второй метод применим только в случае стрелочных графов.

Анализ критического пути с применением вершинных графов - приводится в виде примера 4.

Пример 4

В таблице указана продолжительность выполнения каждой операции проекта, о котором шла речь в примерах 2 и 3. Определим общую продолжительность выполнения проекта.

Операции	Непосредственно предшествующая операция	Время, дней
A	-
B	-
C	-
D	A, B
E	B,C
F	C
G	D, E
H	F, G

Вершинный граф, соответствующий данному проекту, был построен в примере 3.

Предположим, что каждая из исходных операций А, В и С начинается в нулевой момент времени. Это наиболее ранний срок начала этих ES операций. Наиболее ранний срок, к которому их выполнение может быть завершено, определяется следующим образом:

Наиболее ранний срок окончания EF=ES + Продолжительность операции

Обычно найденные значения этих сроков наносятся непосредственно на граф, однако, занесем их сначала в таблицу, чтобы продемонстрировать методику проведения расчетов.

Операция	Продолжи-тельность, дней	Наиболее ранний срок начала	Наиболее ранний срок окончания	Комментарий
A			0 +8 = 8
B			0 + 10 = 10
C			0 + 6 = 6
D			10 + 8 = 18	Нельзя начать, пока не завершены А и В
E			10 +9 = 19	Нельзя начать, пока не завершены В и С
F			14 + 6 = 20	Нельзя начать, пока не завершена С
G			14 + 19 = 33	Нельзя начать, пока не завершены D и E
H			33 + 6 = 39	Нельзя начать, пока не завершены F и G

Наиболее ранние сроки начала и окончания операций занесены в вершинный граф, изображенный на рис. 16.

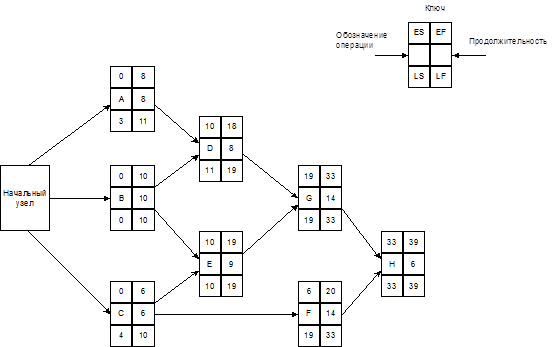
Рис. 16 Вершинный граф для примера 4

Нетрудно заметить, что операция Н завершится на 39-й день, следовательно, это значение дает искомую продолжительность выполнения проекта в целом.

На данном этапе мы еще не можем определить критические операции. Чтобы это осуществить, необходимо для каждой операции рассчитать два срока, ей соответствующие, а именно наиболее поздний срок начала LS и наиболее поздний срок окончания LF операции. В данном случае процедуру расчетов мы начнем с последней операции в графе и предположим, что наиболее поздний и наиболее ранний сроки ее окончания совпадают. Затем вычитанием из этой величины продолжительности выполнения операций находим наиболее поздний срок ее начала. Ход выполнения расчетов показан в таблице:

Таблица Расчет наиболее поздних сроков начала и окончания операций

Операция	Продолжи-тельность, дней	Наиболее поздний срок окончания	Наиболее поздний срок начала	Комментарии
H			39 - 6 = 33
G			33 -14 = 19	G нужно начать до наступления наиболее поз- днего срока начала H
F			33 -14 = 19	F нужно начать до наступления наиболее поз-днего срока начала H
E			19 - 9 = 10	E нужно начать до наступления наиболее поз-днего срока начала G
D			19 - 8 = 11	D нужно завершить до наступления наиболее позднего начала G
C			10 - 6 = 4	С нужно завершить до наступления наиболее позднего срока начала E и F. Нужно использовать наименьший из этих сроков, равный 10 дням.
B			10 - 10 = 0	В нужно завершить до наступления наиболее позднего срока начала D и E. Нужно использовать наименьший из этих сроков, равный 10 дням.
A			11 - 8 = 3	А нужно заверить до наступления наиболее позднего срока начала D

Критической является операция, для которой справедливы следующие соотношения:

ES = LS и EF = LF,

т.е. операция, для которой не существует резерва времени между наиболее ранним сроком ее начала и наиболее поздним сроком ее окончания. Нетрудно заметить, что в данном примере критическими являются операции B, E, G и H. Путь в вершинном графе, соединяющем эти операции, называется B - E - G - H.

Анализ критического пути с применением стрелочных графов. Приведенная выше методика анализа аналогичным образом может использоваться и для стрелочных графов. Значения сроков ES, EF, LS и LF записываются в графе вдоль стрелок, соответствующих операциям (рис. 17):

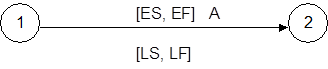
Рис. 17 Нанесение на стрелочный граф сроков, соответствующих операциям.

Можно провести подобный анализ в терминах сроков наступления каждого события. Производится расчет наиболее раннего срока, к которому может завершиться каждое событие. Этот срок называется наиболее ранним сроком события (earliest event time - EET). Общая продолжительность выполнения проекта определяется EET конечного узла. EET исходного события равен нулю.

Для того, чтобы выявить критические операции, необходимо, начиная с конца графа, вычислить наиболее поздние сроки событий (latest event time - LET), к которым события могут закончиться. События, для которых выполняются соотношения

LET _начала - EET _{окончания} + продолжительность = 0

или

EET _начала - LET _{окончания} + продолжительность = 0,

являются критическими.

Пример 5

Применив EET и LET, повторим задачу из примера 4 при условии, что продолжительность выполнения фиктивных операций равна нулю.

В первую очередь для каждого события вычислим значение наиболее раннего срока. Если некоторому событию соответствует более одной операции, появляется проблема выбора соответствующего значения. Поскольку событие считается незавершенным до тех пор, пока не будет завершено выполнение всех составляющих его операций, следует выбрать наибольшее из значений.

Полученные значения сроков наносятся на стрелочный граф, как это показано на рис. 18.

Рис. 18. Стрелочный граф для примера 5 с указанием ЕЕТ и событий.

ЕЕТ последнего события равно 39 дням, которые также определяют общую продолжительность выполнения проекта.

Таблица Расчет значений ЕЕТ для примера 5.

Узел	ЕЕТ, дней	Комментарии
		Начальное событие
	0 + 10 = 10	ЕЕТ узла 1 + продолжительность операции В
	0 + 6 = 6	ЕЕТ узла 1 + продолжительность операции С
	0 + 8 = 8 или 10 + 0 = 10*	ЕЕТ узла 1 + продолжительность операции А ЕЕТ узла 2 + продолжительность фиктивной операции Выбирается максимальный срок, т.е. 10 дней
	10 + 0 = 10*   или 6 + 0 = 6*	ЕЕТ узла 2 + продолжительность фиктивной операции ЕЕТ узла 3 + продолжительность фиктивной операции Выбирается максимальный срок, т.е. 10 дней
	10 + 8 = 18 или 10 + 9 = 19*	ЕЕТ узла 4 + продолжительность операции D ЕЕТ узла 5 + продолжительность операции E Выбирается максимальный срок, т.е. 19 дней
	19 + 14 = 33* или 6 + 14 = 20	ЕЕТ узла 6 + продолжительность операции G ЕЕТ узла 3 + продолжительность операции F Выбирается максимальный срок, т.е. 33 дня
	33 + 6 = 39	ЕЕТ узла 7 + продолжительность операции Н

*

Чтобы определить критические операции, будем двигаться по графу, начиная с конечного узла и вычисляя LET каждого события. Предположим, что для конечного события ЕЕТ = LET. Если в некоторый узел входит более одной стрелки, то возникает проблема выбора значения LET. Так как событие должно завершится к сроку, удовлетворяющему всем наиболее поздним срокам начала событий, которые выходят из данного узла для LET, следует выбрать наименьшее значение.

Найденные значения сроков наносятся на стрелочный граф, изображенный на рис. 18

Операция является критической, если для нее справедливы следующие соотношения:

ЕЕТ _начала = LET _начала

и

ЕЕТ _{окончания} = LET _{окончания}

LET _{окончания} - ЕЕТ _начала - Продолжительность= 0.

Из рис. 18 видно, что критическими, как и ранее являются операции В, Е, G и H.

Таблица Расчет значений LET для примера 5.

Узел	LET, дней	Комментарии
		Конечный узел LET = ЕЕТ
	39 - 6 = 33	LET узла 8 - продолжительность операции Н
	33 - 14 = 19	LET узла 7 - продолжительность операции G
	19 - 9 = 10	LET узла 6 - продолжительность E
	19 - 8 = 11	LET узла 6 - продолжительность операции D
	10 - 0 = 10** или 33 - 14 = 19	LET узла 5 - продолжительность фиктивной операции или LET узла 7 - продолжительность операции F Выбирается минимальный срок, т.е. 10 дней
	10 - 0 = 10**   или 11 - 0 =11	LET узла 5 - продолжительность фиктивной операции или LET узла 4 -продолжительность фиктивной операции Выбирается минимальный срок, т.е. 10 дней
	11 - 8 = 3 или 10 - 10 = 0** или 10 - 6 = 4	LET узла 4 - продолжительность операции А или LET узла 2 -продолжительность операции В или LET узла 3 - продолжительность операции С Выбирается минимальный срок, т.е. 0 дней

**

Дата добавления: 2014-01-20