Алгебраические методы синтеза

Алгебраические методы синтеза для одномерной САУ строятся на определении вида и параметров передаточной функции изменяемой части САУ в выражении

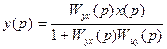, (1.10)

где х(р), у{р) — соответствующие преобразования Лапласа x(t) и y(t) (начальные условия считаем нулевыми); W_yx (р), W_uy(p) —передаточные функции неизменяемой части САУ (объекта управления) и изменяемой ее части соответственно; и — управляющее воздействие; y(р)— желаемый (заданный) вид решения системы на заданное входное воздействие х(р).

Поскольку Wyx(p) связывает входное воздействие х(р) и реакцию системы у(р), при заданных х{р) и у(р) получаем алгебраическое уравнение

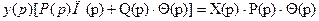(1.11)

в котором Р{р), Q(p) суть известные заданные полиномы от р,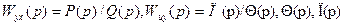, - полиномы от р, которые необходимо построить.

В общем случае уравнение (1.11) представляет собой одно уравнение с двумя неизвестными Θ(р) и П(р) и относится к диофантовым (Диофант — древнегреческий математик) уравнениям. Для нахождения решения этого уравнения добавляются условия устойчивости системы (1.10) физической реализуемости изменяемой части CAP W_uy (p). В последнем случае, в частности, требуется, чтобы степень полинома Θ(р) была выше степени полинома П(р). Эту систему уравнений следует дополнить условиями устойчивости, составляемыми по критерию Рауса R_k(a_i)>0, где а_i — коэффициенты характеристического полинома 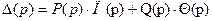в (1.10); R_k(a_i) —коэффициенты первого столбца таблицы Рауса.

Вместо неравенств можно получить уравнения для условий устойчивости. При этом необходимо задать степень устойчивости системы (1.10) .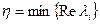

Тогда уравнение соответствующее Δ(р), преобразуется к смещенному характеристическому уравнению

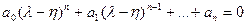
После пересчета коэффициентов это уравнение примет вид

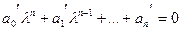, (1.12)

где 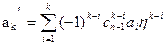; k — номер коэффициента; 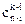-число сочетаний по k-i из n-i.

Желаемый процесс у(t) можно сформировать из операторного изображения переходных характеристик, задаваемого в обобщенном виде

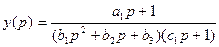
Придавая параметрам a₁,b₁,b₂,b₃,c₁ числовые значения от нуля до предельных значений, можно получать колебательные, апериодические и другие формы переходных процессов. В частности, при c₁=0 изображение желаемого процесса по Лапласу имеет вид

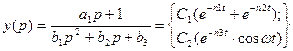(1.13)

соответственно при вещественных и комплексных полюсах. В этих выражениях С1, С2 определяют величину динамической ошибки σ;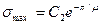, где 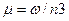— колебательность процесса; запасы устойчивости определяются величинами n1 (n1<n2) и n3.

Рассматривая наиболее тяжелый режим работы САУ — отработку ступенчатых воздействий х(р) = 1/р, задачу синтеза можно свести к решению алгебраических уравнений (1.11), (1.12) относительно неизвестных коэффициентов полиномов Θ(р), П(р). В общем случае подобные уравнения решаются с помощью алгоритма Евклида. Распространение этого метода на многомерные системы сводится к решению матричного алгебраического уравнения для многомерной САУ

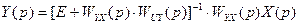, (1.14)

где Y(р), X(р), W_YX(p), W_UY (p) —векторы и матрицы, соответствующие выходным и входным воздействиям. Если заданы виды возмущающих воздействий Х(р), желаемый вид выходных процессов CAY Y(p) и неизменяемая часть САУ W_YX(p), то из матричного уравнения (1.14) можно найти матрицу W_UY(p) как результат решения системы алгебраических уравнений (1.14). В этом случае, так же как и в скалярном, к уравнениям (1.14) следует добавить условия устойчивости системы (1.14) и физической реализуемости изменяемой части САУ W_UY(P).

Рассмотренный подход развит в виде метода полиномиальных уравнений, который может быть применен как к непрерывным, так и к цифровым регуляторам САУ. В последнем случае этот метод наиболее эффективен. По существу он является численным методом решения определенного круга вариационных задач и позволяет единообразным путем, учтя условия физической реализуемости и устойчивости САУ, получить в явной форме выражение оптимальной передаточной функции регулятора Wuy. Важным достоинством метода является то, что оптимальность здесь понимается не только в смысле быстродействия, но и в смысле компенсации нежелательных отклонений САУ от заданного движения, что приближает задачу синтеза к инженерной постановке в смысле критериев (1.8)—(1.9).

Применение метода полиномиальных уравнений требует перехода к «дискретной модели» непрерывной части системы.

Для удобства последующего изложения рассмотрим алгоритм метода применительно к одномерной системе (1.10). Осуществляя преобразование функции (1.10), представим ее в виде

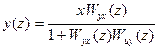(1.15)

Wyx(z)=P(z)/Q(z) — заданная передаточная z-функция неизменяемой части системы; х*Wyx(z)=L(z)/R(z)— передаточная z-функция участка контура регулирования между точкой приложения возмущающего воздействия x(z) и координатой у(z); Wuy(z) —искомая функция регулятора.

Для компенсации «нежелательных» полюсов и нулей в передаточной функции Wyx(z) применяется операция факторизации. Эта операция состоит в следующем. Представим функцию Wyx(y) в виде

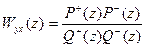, (1.16)

где 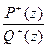—дробно-рациональная функция, имеющая нули и полюсы в области устойчивости, в данном случае — внутри круга единичного радиуса |z| = 1, а 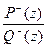имеет нули и полюсы вне области устойчивости.

Представим искомую функцию Wuy(z) произведением трех сомножителей:

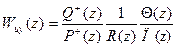(1.17)

где Θ,П— неизвестные полиномы.

Подставляя (1.16), (1.17) в (1.15), найдем

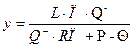(1.18)

Определим неизвестные полиномы Θ и П как минимальное решение (т. е. решение, при котором степени полиномов Θ и П наименьшие) полиномиального уравнения

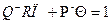(1.19)

Тогда y(t) будет процессом конечной минимальной длительности при возможности одновременного обеспечения устойчивости и минимума динамической ошибки. Подставляя найденные П и Θ в (1.17), находим искомую функцию Wuy(z).

При использовании наряду с принятыми дополнительными критериями синтеза, например минимальной суммарной квадратичной ошибки, как выражение (1.17), так и полиномиальное уравнение (1.19) могут значительно усложняться, что, однако, не носит принципиального характера. Метод позволяет весьма точно учитывать ограничения со стороны неизменяемой части системы, путем привлечения аппарата линейного программирования. Задачи статистического синтеза также сводятся к решению систем полиномиальных уравнений. Применительно к задачам синтеза регуляторов САУ метод полиномиальных уравнений имеет ряд преимуществ: простоту машинной ориентации метода, практическое отсутствие вычислительных трудностей и возможность синтеза систем, обладающих свойством удовлетворять совокупности различных требований (достигается абсолютный экстремум по одному из критериев при относительных экстремумах по остальным). Результатом синтеза является передаточная z-функция или эквивалентное разностное уравнение, реализуемые в дальнейшем на микропроцессоре САУ.

Дата добавления: 2014-01-20