
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет водонагревателя – аккумулятора с водяным обогревом
|
|
|
|
На рис. 3.6 изображены схемы аппарата и соответствующий ей график изменения температур греющей и нагреваемой воды в зависимости от времени [2,4].
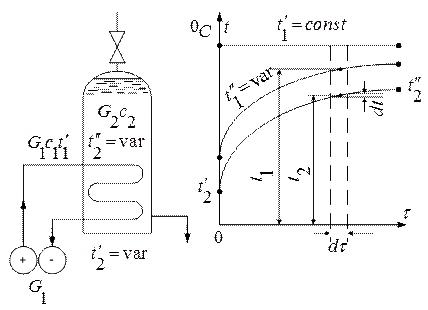
Рис. 3.6. График изменения температур в водонагревателе-аккумуляторе с водяным обогревом.
Особенность режима работы такого аппарата состоит в том, что температура греющей воды на выходе из аппарата 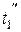 возрастает во времени при постоянных расходе G 1и начальной температуре. Это объясняется тем, что вода в аккумуляторе нагревается и для ее последующего нагрева требуется все меньший и меньший перепад температуры. Расчет при этом усложняется, так как приходится использовать две переменные во времени t 1и t 2. Дифференциальные уравнения теплопередачи и теплового баланса запишутся в виде
возрастает во времени при постоянных расходе G 1и начальной температуре. Это объясняется тем, что вода в аккумуляторе нагревается и для ее последующего нагрева требуется все меньший и меньший перепад температуры. Расчет при этом усложняется, так как приходится использовать две переменные во времени t 1и t 2. Дифференциальные уравнения теплопередачи и теплового баланса запишутся в виде

 , (3.6)
, (3.6)
где G 1 c 1и G 2 c 2 - теплоемкости массовых расходов теплоносителей;  - элемент времени, в течение которого температура воды повышается на dt, с; k - коэффициент теплопередачи,
- элемент времени, в течение которого температура воды повышается на dt, с; k - коэффициент теплопередачи,  ; F — поверхность нагрева, м2;
; F — поверхность нагрева, м2; 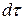 - средняя логарифмическая разность температур, она определяется как
- средняя логарифмическая разность температур, она определяется как
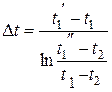 ,
,
где  , t 1 и t 2температуры греющей и нагреваемой воды в рассматриваемый промежуток времени
, t 1 и t 2температуры греющей и нагреваемой воды в рассматриваемый промежуток времени 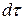 .
.
Подставив в уравнение (3.6) выражение для  , получим:
, получим:
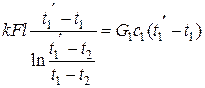 .
.
Определим температуру t 1:

Введем обозначение A = kF/G 1 с 1.
Температура греющей воды на выходе из аппарата
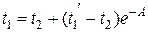 . (3.7)
. (3.7)
Подставив в уравнение (3.6) значение переменной t 1из уравнения (3.7) и сделав преобразования, получим:
 ;
;
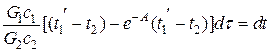 ;
;
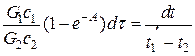 .
.
Левую часть уравнения интегрируем в пределах от 0 до 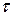 , а правую - в пределах от начальной температуры
, а правую - в пределах от начальной температуры  до конечной
до конечной 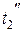 :
:
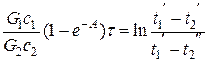 . (3.8)
. (3.8)
Из уравнения (3.8) определяется удельная производительность аппарата:
 ;
;
 ;
;
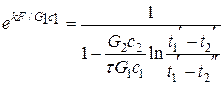 ;
;
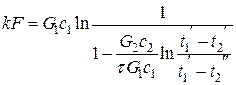 . (3.9)
. (3.9)
где kF и коэффициент теплопередачи k определяются по формуле для плоской стенки (2.12). По известным kF и k однозначно определяется поверхность нагрева аппарата F = kF/k.
Средняя температура воды определяется приближенно по формуле
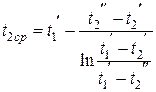 . (3.10)
. (3.10)
По значению температуры 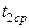 можно определить коэффициент теплоотдачи от стенки к нагреваемой воде.
можно определить коэффициент теплоотдачи от стенки к нагреваемой воде.
Среднее значение температуры греющей воды находится по формуле
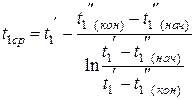 , (3.11)
, (3.11)
где 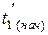 и
и 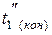 - температуры греющей воды на выходе аппарата в начальный момент и в конце процесса.
- температуры греющей воды на выходе аппарата в начальный момент и в конце процесса.
Если поверхность аппарата задана, то конечная температура нагреваемой воды 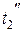 в зависимости от времени нагрева определяется из уравнения (3.8):
в зависимости от времени нагрева определяется из уравнения (3.8):
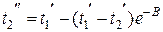
где
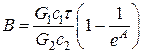 .
.
Средняя температура греющей воды на выходе определяется из уравнения теплового баланса
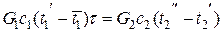 ,
,
откуда
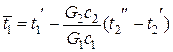 . (3.12)
. (3.12)
Принагревании воды или других сред в аппаратахпериодического действия часть теплоты греющего теплоносителя расходуется на нагревание корпуса аппарата и тепловой изоляции и компенсацию тепловых потерь в окружающую среду. Для учета затрат теплоты на нагрев конструкции в полученные выше формулы вместо 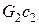 обычно подставляют полную теплоемкость аппарата, заполненного нагреваемой средой:
обычно подставляют полную теплоемкость аппарата, заполненного нагреваемой средой:  , где
, где 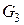 и
и 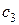 ,
, 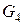 и
и  - массы и удельные теплоемкости элементов конструкции аппарата и изоляции.
- массы и удельные теплоемкости элементов конструкции аппарата и изоляции.
3.3. Определение коэффициента теплопередачи для водонагревателя – аккумулятора.
Коэффициенты теплопередачи определяются по формулам 2.11, 2.12, как для аппаратов непрерывного действия.
Коэффициент теплоотдачи от греющего теплоносителя к стенкам трубы определяется как для аппаратов непрерывного действия по ранее рассмотренным уравнениям 2.15 - 2.21.
Особенностью расчета аппаратов периодического действия является то, что теплоотдача от поверхности теплообмена к нагреваемой среде осуществляется при естественной конвекции.
Особенностью водонагревателей – аккумуляторов по сравнению с другими, рассмотренными ранее теплообменниками непрерывного действия является то, что теплоотдача к нагреваемой воде в них осуществляется в большинстве случаев при ее естественной конвекции.
Коэффициент теплоотдачи от вертикальных и горизонтальных труб при естественной конвекции жидкости и газа в большом объеме может быть определен по формуле М. А. Михеева
 ,
,
где Gr – число Грасгоффа, 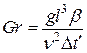 ; Pr – число Прандтля.
; Pr – число Прандтля.
Для расчетов по уравнению физические свойства берут при средней температуре пограничного слоя 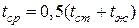 . В качестве определяющего геометрического размера принимают высоту вертикальной поверхности или наружный диаметр трубы. Для горизонтальных труб
. В качестве определяющего геометрического размера принимают высоту вертикальной поверхности или наружный диаметр трубы. Для горизонтальных труб 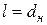 , для вертикальных труб или рубашки
, для вертикальных труб или рубашки 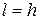 , h – высота вертикальной поверхности теплообмена.
, h – высота вертикальной поверхности теплообмена.
Формула применима для жидкостей и газов при 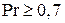 . В ней обозначено:
. В ней обозначено:
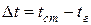 ;
;  ,
,
где 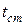 - температура теплоотдающей поверхности стенки;
- температура теплоотдающей поверхности стенки; 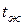 - средняя температура жидкости;
- средняя температура жидкости; 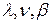 - физические константы жидкости (коэффициенты теплопроводности, кинематической вязкости и объемного расширения жидкости) при температуре пограничного слоя
- физические константы жидкости (коэффициенты теплопроводности, кинематической вязкости и объемного расширения жидкости) при температуре пограничного слоя  ; l – характерный размер: для горизонтальных труб
; l – характерный размер: для горизонтальных труб 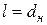 (
( - наружний диаметр трубки), для вертикальных трубок
- наружний диаметр трубки), для вертикальных трубок 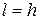 ; h – высота трубки.
; h – высота трубки.
Величины А и m зависят от произведения GrPr В практических расчетах принимают следующие соотношения (табл. 3.1)
Таблица 3.1. Значение констант уравнения 3.13
| Режим | GrPr | А | m |

| 1,18 | 1/8 | |
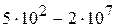
| 0,54 | 1/4 | |
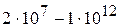
| 0,135 | 1/3 |
При первом режиме теплота передается в основном теплопроводностью, так как теплоотдача слабо зависит от величины GrPr. При втором режиме теплота передается в основном свободной (естественной) конвекцией при ламинарном течении теплоносителя. При третьем режиме теплота передается свободной конвекцией при смешанном и турбулентном движении теплоносителя.
В аппаратах с мешалками, имеющими поверхность теплообмена в форме рубашек или змеевиков, процесс теплоотдачи из-за перемешивания жидкости протекает очень интенсивно. Это происходит вследствие значительной скорости обтекания циркуляционными токами жидкости поверхностей теплообмена. Интенсивное перемешивание обеспечивает равномерность температуры практически по всему объему среды, т. е. в этих аппаратах гидродинамическая структура потоков наиболее близка к модели идеального смешения.
Коэффициент теплоотдачи в аппаратах со змеевиками, рубашками и мешалкой можно определить по уравнению
 , (3.14)
, (3.14)
где 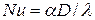 ,
,  - центробежный критерий Рейнольдса; D -диаметр аппарата;
- центробежный критерий Рейнольдса; D -диаметр аппарата;  - диаметр окружности, описываемый, мешалкой; n -частота вращения мешалки;
- диаметр окружности, описываемый, мешалкой; n -частота вращения мешалки; 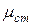 - вязкость жидкости при температуре стенки
- вязкость жидкости при температуре стенки 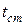 аппарата или змеевика;
аппарата или змеевика; 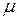 - вязкость жидкости при средней температуре -
- вязкость жидкости при средней температуре -  .
.
Значение остальных физических констант следует брать при средней температуре 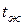 жидкости.
жидкости.
Для аппаратов с рубашками А = 0,36, т = 0,67; для аппаратов со змеевиками А = 0,87, т = 0,62; в качестве определяющего размера принимается наружный диаметр змеевика.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 4413; Нарушение авторских прав?; Мы поможем в написании вашей работы!