Перегонка жидкостей

Лекция №13

При проведении многих химико-технологических процессов часто встречаются задачи разделения жидких гомогенных (однородных) смесей на составляющие компоненты. Для проведения таких процессов наибольшее применение получила перегонка жидких смесей.

Перегонка жидкостей представляет собой процесс, в котором разделяемая жидкая смесь нагревается до кипения, а образующийся пар отбирается и конденсируется. В результате получают жидкость – конденсат, состав которой отличается от состава начальной смеси. Повторяя много раз процессы испарения конденсата и конденсации, можно практически полностью разделить исходную смесь на чистые составные части (компоненты).

Процесс перегонки основан на том, что жидкости, составляющие смесь, обладают различным давлением (упругостью) пара при одной и той же температуре. Поэтому состав пара, а следовательно, и состав жидкости, получающейся при конденсации пара, будут несколько отличаться от состава начальной смеси: легколетучего (или низкокипящего – НК) компонента в паре будет содержаться больше, чем в перегоняемой жидкости. Очевидно, что в неиспарившейся жидкости концентрация труднолетучего (или высококипящего – ВК) компонента при этом должна увеличиться.

В простейшем случае перегонка почти не отличается от выпарки. Но выпарке подвергаются растворы, состоящие из летучего растворителя и практически нелетучего растворенного вещества, а при перегонке в пар переходят и растворитель и растворенное вещество.

Перегонка является одним из важнейших технологических процессов разделения и очистки жидкостей и сжиженных газов в химической, нефтехимической, нефтеперерабатывающей, фармацевтической, пищевой и других отраслях промышленности.

Перегонку подразделяют на два основных вида: простую перегонку (или дистилляцию) и ректификацию. К простой перегонке относят также перегонку с водяным паром и молекулярную дистилляцию.

Под простой перегонкой понимают процесс однократного частичного испарения исходной жидкой смеси и конденсации образующихся при этом паров. Ее применяют для разделения смесей, представляющих собой легколетучее вещество с некоторым содержанием весьма труднолетучих веществ. Обычно простую перегонку используют для предварительного разделения, очистки веществ от примесей, смол, загрязнений. При этом сконденсированные пары называют дистиллятом, а оставшуюся неиспаренную жидкость – остатком.

Ректификация – наиболее полное разделение смесей жидкостей, целиком или частично растворимых друг в друге. Процесс заключается в многократном взаимодействии паров с жидкостью – флегмой, полученной при частичной конденсации паров.

Равновесие в системах жидкость – пар [1]

В общем случае жидкая смесь может состоять из нескольких компонентов. В простейшем случае – из двух, например из компонентов А и В. Характер поведения жидкой смеси зависит главным образом от природы составляющих ее веществ и давления.

По степени растворимости компонентов смеси жидкости подразделяют на взаиморастворимые в любых соотношениях, частично растворимые и практически взаимонерастворимые. В свою очередь смеси со взаиморастворимыми компонентами в любых соотношениях делятся на идеальные растворы, которые подчиняются закону Рауля; так называемые нормальные растворы – жидкие смеси, частично отклоняющиеся от закона Рауля, но не образующие смесей с постоянной температурой кипения (азеотропов); неидеальные растворы – жидкости со значительными отклонениями от закона Рауля, в том числе смеси с постоянной температурой кипения (азеотропы). Полностью взаимонерастворимых жидкостей нет, обычно все жидкости хотя бы в незначительных количествах, но растворяются друг в друге. Однако в этих случаях на практике для удобства принимают такие жидкости взаимонерастворимыми.

Идеальные смеси

Для идеальных растворов характерно то, что сила взаимодействия между всеми молекулами (одноименными и разноименными) равна. При этом общая сила, с которой молекула удерживается в смеси, не зависит от состава смеси. Очевидно, что парциальное давление в этом случае должно зависеть лишь от числа молекул, достигающих в единицу времени поверхности жидкости со скоростью, необходимой для преодоления сил внутреннего притяжения молекул, т.е. при данной температуре давление соответствующего компонента возрастает пропорционально его содержанию в жидкой смеси (закон Рауля). Для бинарной смеси парциальное давление компонентов смеси А и В будет равно:

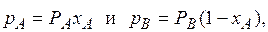(3.1)

где P_A – упругость пара чистого низкокипящего компонента А; P_B – упругость пара чистого высококипящего компонента В; x_A – молекулярная доля компонента А в жидкости; () – молекулярная доля компонента В в жидкости.

Так как 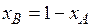, то по законам Рауля и Дальтона

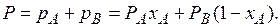(3.2)

Из уравнений (3.1), (3.2), выражающих законы Рауля и Дальтона, видно, что при постоянной температуре парциальное давление компонентов, а также общее давление паров над смесью находятся в линейной зависимости от x_A – молярного содержания низкокипящего компонента в жидкости. На рис. 3.1 при 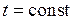прямые ОВ и СА выражают изменения парциальных давлений компонентов 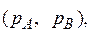а прямая АВ – изменение общего давления над раствором. Вертикальные отрезки СВ и ОА соответствуют давлению насыщенных паров чистых компонентов .

Температура кипения смеси заданного состава x_A является функцией давления пара. Для того чтобы определить ее, строят по значениям давлений насыщенных паров чистых компонентов (из справочников) изобары АВ, А ₁ В ₁, А ₂ В ₂ и т.д., выражающие общее давление паров при температурах t, t ₁, t ₂ и т.д. Линии парциальных давлений 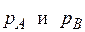получают, соединяя прямыми точки А, А ₁, А ₂ и т.д. с точкой С, точки В, В ₁, В ₂ и т.д. – с точкой О. Далее проводят горизонтальную прямую MN, соответствующую внешнему давлению р. Из точки на оси абсцисс, соответствующей x_A, восстанавливают вертикаль до пересечения с прямой MN в точке D, через которую проходит изотерма .

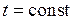При этой температуре общее давление пара смеси равно внешнему давлению, и следовательно, смесь состава x_A кипит при температуре t. Аналогично можно определить температуру кипения смеси состава 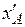, равную t ₁, смеси состава 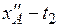и т.д.

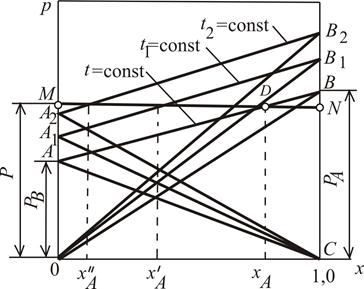
Рис. 3.1. Изобары парциальных давлений компонентов и общего

давления (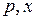– диаграмма)

Для технических расчетов наиболее важной является диаграмма t – x, y, так как обычно процессы перегонки в промышленных аппаратах протекают при Р = const, т.е. в изобарных условиях. На этой диаграмме (рис. 3.2) по оси абсцисс отложены концентрации жидкой x и паровой y фаз, отвечающие различным температурам.

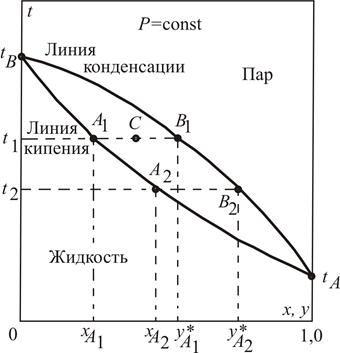
Рис. 3.2. Фазовая диаграмма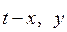

По закону Дальтона 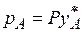, и тогда (с учетом 3.1)

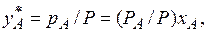(3.3)

где 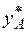– состав пара, равновесный с жидкостью, но

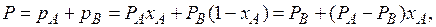
тогда

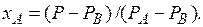(3.4)

По уравнению (3.4) по известным 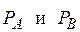при заданной температуре 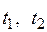и т.д. находят 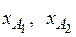и т.д., а затем по уравнению (3.3) – соответствующие значения 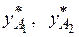и т.д., и по найденным точкам строят линии кипения жидкости (кривая 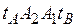) и конденсации паров (кривая 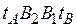). Уравнение (3.4) устанавливает связь между концентрациями (по жидкости) и заданными давлениями (общим Р и насыщенных паров 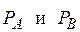). Отрезки А ₁ В ₁, А ₂ В ₂ и т.д., соединяющие точки равновесных составов жидкой и паровой фаз, являются изотермами.

Отметим, что точки, лежащие на кривой 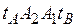, отвечают жидкой фазе, находящейся при температуре кипения. Очевидно, что любая точка, лежащая ниже этой кривой, характеризует систему, состоящую только из жидкой фазы. Аналогично, любая точка, лежащая выше кривой 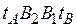, характеризует систему, температура которой выше температуры начала конденсации пара, т.е. пары в этой точке являются перегретыми, и система состоит только из паровой фазы. Точки, находящиеся между кривыми кипения и конденсации (например, точка С на рис. 3.2), характеризуют системы, температуры которых выше температуры кипения жидкости данного состава и ниже температуры конденсации паров этого же состава. Таким образом, эти точки отвечают равновесным парожидкостным системам (двухфазная область). Диаграмма 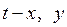называется фазовой диаграммой.

На практике часто применяют y, x -диаграмму равновесия, в которой на оси абсцисс отложены составы жидкости x, по оси ординат – равновесные с этим значением x составы паров y (рис. 3.3).

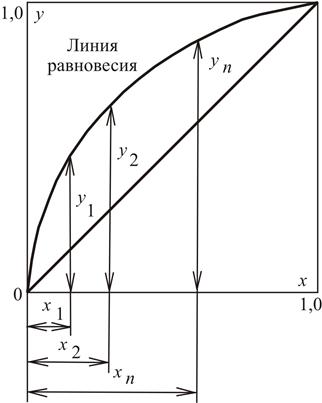
Рис. 3.3. Диаграмма равновесия для бинарной смеси

Зависимость y от x выражена линией равновесия. Кроме этой линии на диаграмме приведена вспомогательная диагональ. Линия равновесия расположена выше диагонали, следовательно, ординаты точек на линии равновесия выше их абсцисс, т.е. пары всегда обогащены низкокипящим компонентом. Чем ближе линия равновесия к диагонали, тем меньше различаются составы пара и жидкости и тем труднее разделяется смесь при перегонке и ректификации.

Кривая равновесия для растворов, подчиняющихся закону Рауля, может быть построена по уравнению

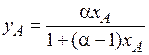, (3.5)

где 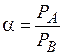– относительная летучесть компонентов. Чем больше числовое значение 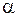, тем сильнее отклоняется кривая от диагонали, тем больше различие в составе пара и жидкости и тем легче разделить смесь на компоненты. На диаграмме – 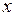фазовые точки пара и жидкости сливаются в одну точку, всегда лежащую на кривой равновесия.

Кривая равновесия и диагональ ограничивают область взаимного существования двух фаз. Выше кривой равновесия расположена область пара, а ниже – область жидкости.

Взаимное расположение кривых на фазовых диаграммах t – x – y и y – x как для идеальных, так и для реальных систем может быть определено с помощью законов Коновалова. Законы Коновалова устанавливают связи между изменениями состава, давления или температуры в двухфазных системах, они лежат в основе теории перегонки и ректификации бинарных смесей.

Первый закон Коновалова формулируется так: пар обогащается тем компонентом, при добавлении которого к жидкости повышается давление пара над ней или снижается ее температура кипения, или пар всегда более обогащен НК, чем соответствующая ему равновесная жидкая фаза.

Первый закон Коновалова дополняется первым правилом Вревского,отражающим влияние температуры на равновесные составы фаз: при повышении температуры бинарной смеси в парах возрастает относительное содержание того компонента, парциальная молярная теплота испарения которого больше.

Это можно проиллюстрировать с помощью фазовой диаграммы (рис. 3.2). Для идеальной смеси очевидно, что при одной и той же температуре t содержание НК в парах 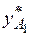(точка В ₁) больше его содержания 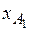в равновесной с парами жидкости (точка А ₁). При добавлении к смеси НК ее температура кипения снижается, но содержание НК в паре остается выше, чем в жидкости.

Реальные смеси

Реальные жидкие смеси могут значительно отклоняться от закона Рауля. Если зависимость полного давления (или сумма парциальных давлений) паров от состава жидкой смеси проходит выше линий, характеризующих те же зависимости для идеальных смесей (рис. 3.4), то такое отклонение называют положительным, если ниже – отрицательным отклонением от закона Рауля.

Эти отклонения определяются изменением активности молекул в растворе, диссоциацией, гидратацией и др. Степень отклонения реальной системы от закона Рауля выражают величиной коэффициента активности

.

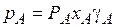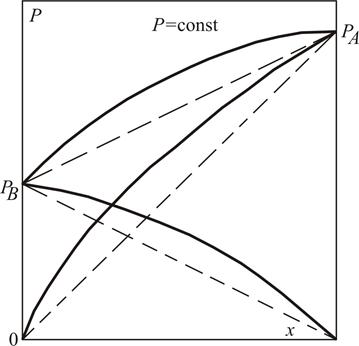
Рис. 3.4. Диаграмма р – x для смеси с положительным отклонением от

закона Рауля (пунктиром показаны соответствующие линии

для идеального раствора)

Для смесей с положительным отклонением от закона Рауля 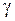> 1, для смесей с отрицательным отклонением – 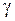< 1. Отметим, что определение значений 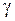часто затруднительно, поэтому диаграммы y – x обычно строят по экспериментальным (справочным) данным.

Для многих реальных смесей отклонение от закона Рауля настолько существенно, что приводит к качественно новому состоянию системы, а на фазовых диаграммах р – x и t – x, y появляются (рис. 3.5. б, в) относительный максимум или минимум. При этом кривые жидкости и пара соприкасаются друг с другом в экстремальных точках, в которых составы равновесных фаз одинаковы. Такие смеси называют азеотропными, или азеотропами. Их основная особенность состоит в том, что при испарении такая смесь (азеотроп) не изменяет своего состава, поэтому для ее разделения требуются специальные методы перегонки. Точка, в которой кривая состава фаз пересекает диагональ на диаграмме y, x, называют азеотропной точкой А_т. Ей соответствует состав смеси, которая при данном давлении не может быть разделена перегонкой на составляющие ее компоненты (рис. 3.5).

Рис. 3.5. Фазовые диаграммы равновесия жидкость – пар для идеальной (а) и реальной (б, в) систем

Эта особенность азеотропных смесей постулируется вторым законом Коновалова, который можно сформулировать следующим образом: если давление и температура сосуществования двух бинарных фаз имеют экстремум (максимум или минимум), то составы фаз одинаковы. Это справедливо для фаз любой природы. Для систем жидкость – пар второй закон Коновалова определяет основное свойство азеотропов.

При изменении внешних условий – температуры (или давления) значение 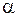изменяется различно по разные стороны от точки азеотропа; одна часть «рыбки» (рис. 3.5, б,) должна становиться шире, другая уже. Очевидно, что в части диаграммы, где в паре содержится больше, чем в растворе, компонента с меньшей теплотой испарения, при понижении температуры (давления) 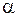увеличивается.

Смещение состава азеотропов при изменении внешних условий определяется вторым законом Вревского: если давление (температура) системы жидкость – пар имеет максимум, то при повышении температуры в азеотропной смеси возрастает концентрация того компонента, парциальная молярная теплота испарения которого больше, а если давление (температура) системы раствор – пар имеет минимум, то при повышении температуры в азеотропной смеси возрастает концентрация компонента с меньшей теплотой испарения. Этот закон был установлен Вревским строго термодинамически, но сформулирован в качественной форме. Он определяет возможность разделения азеотропных смесей изменением давления при перегонке. При этом точка азеотропа на диаграмме y – x перемещается и в принципе может совпасть, например, с правым верхним углом диаграммы. Это позволит разделить азеотропную смесь перегонкой.

Смеси жидкостей, нерастворимых друг в друге

Когда смешаны две взаимонерастворимые жидкости, то каждая из них полностью сохраняет свои свойства. Такая смесь легко может быть разделена на составные части механическим путем, при помощи отстаивания. Система состоит из двух компонентов и трех фаз и, следовательно, обладает одной степенью свободы. Это указывает на то, что каждой определенной температуре смеси будет соответствовать вполне определенное давление и каждый из компонентов будет вести себя так, как будто он находится один в чистом виде.

Иными словами, в смеси, состоящей из взаимно нерастворимых жидкостей, парциальное давление каждого компонента не зависит от его содержания в смеси и равно давлению паров чистого компонента при той же температуре (рис. 3.6, а):

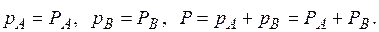
Диаграмма равновесия несмешивающихся жидкостей при постоянном давлении изображена на рис. 3.6, а, б, где по оси ординат отложена температура, а по оси абсцисс – содержание компонентов А и В. В точке а существует только компонент А, а в точке b – только компонент В.

Горизонталь ab на диаграмме ограничивает область существования смеси жидкостей А и В,а точка с соответствует состоянию кипения смеси, причем температура кипения смеси лежит ниже температуры кипения отдельных компонентов.

Как видно из диаграммы, температура кипения смеси всегда меньше температуры кипения чистых компонентов.

Рис. 3.6. Диаграммы p – x; t – x, y; y – x для нерастворимых жидкостей

Состав пара определяется соотношением

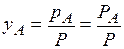
и не зависит от состава жидкости.

Линии парциальных и полного давлений на 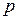– x диаграмме, а также линия кипения на t – x, y диаграмме изображаются горизонтальными прямыми. Линия конденсации на t – x, y диаграмме изображается линией dce. Точка с с абсциссой, равной составу пара, соответствует азеотропной смеси с минимальной температурой кипения (рис. 3.6, б). Линия кипения изображается линией аb. Примером смеси с нерастворимыми компонентами может служить смесь бензол – вода.

На диаграмме равновесия (рис. 3.6, в) показано, что состав пара не зависит от состава жидкости, что является характерным для рассматриваемых смесей.

Смеси частично растворимых жидкостей [1]

Особенностью этих смесей является то, что в зависимости от содержания компонентов жидкость может быть либо однородной, либо состоящей из двух несмешивающихся слоев.

Если, например, постепенно прибавлять к воде эфир, то вначале эфир будет растворяться в воде, так что получится однородная жидкость. Это будет продолжаться до тех пор, пока не образуется насыщенный раствор эфира в воде (состав 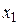на рис. 3.7, а, б).

Рис. 3.7. Фазовые диаграммы (а, б) равновесия для систем с ограниченной взаимной растворимостью

После этого дальнейшие порции эфира не будут растворяться, причем жидкость разделится на два слоя, из которых один представляет собой насыщенный раствор эфира в воде, а другой – насыщенный раствор воды в эфире. Однако при дальнейшем прибавлении эфира достигается такое соотношение между количеством воды и эфира в смеси, которое соответствует растворимости воды в эфире (состав x ₂ на рис. 3.7, а, б). При этом жидкость снова станет однородной и будет представлять собой насыщенный раствор воды в эфире. После этого жидкость будет оставаться однородной и при дальнейшем прибавлении эфира.

Характер диаграмм t – x, y и y – x будет изменяться в зависимости от того, является ли жидкость однородной или состоит из двух слоев (рис. 3.7). В первом случае будут иметь место закономерности, справедливые для смесей взаимно растворимых жидкостей, а во втором – закономерности, справедливые для смесей жидкостей, нерастворимых друг в друге.

В интервале состава 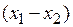– жидкость будет неоднородной. Подобные смеси имеют азеотропную точку (точка А на рис. 3.7).

Дата добавления: 2014-01-20