Правила построения рядов распределения аналогичны правилам построения группировки

Распределение работников строительной фирмы по уровню дохода в январе 2004г.

Примером такого ряда распределения может служить распределение работников организаций по уровню дохода.

Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, распределение семей по числу детей, распределение рабочих по тарифному разряду. В случае непрерывной вариации признак может принимать определенные значения, отличающиеся друг от друга на сколь угодно малую величину. Построение интервальных вариационных рядов целесообразно при непрерывной вариации признака, а также, если дискретная вариация проявляется в широких пределах.

В зависимости от характера вариации признака различают дискретные и интервальные ряды.

Группы работников по уровню дохода, руб.	Число работников, чел.	Удельный вес, % к итогу
До 5000
5000-1000
10000-15000
15000 и более
Итого		100,0

Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются значения вариантов, а по оси ординат величины частот. Полученные на пересечении абсцисс и ординат точки соединяют прямыми линиями и получают ломанную линию, называемую полигоном частот. Для замыкания полигона крайние точки (слева и справа на ломанной линии) соединяют с точками на оси абсцисс и получают многоугольник.

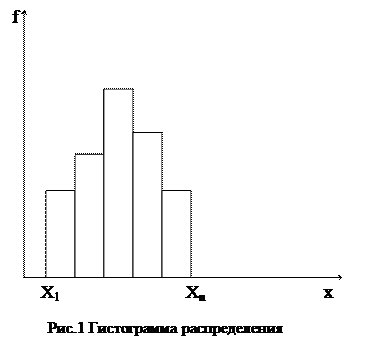
Гистограмма (рис.1) применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам.

Если середины верхних сторон прямоугольников соединить прямыми, то гистограмма может быть преобразована в полигон распределения (рис.2)

При построении гистограммы вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения (частота, рассчитанная на единицу ширины интервала) признака в соответствующих интервалах. Это необходимо сделать для того, чтобы получить возможности сравнивать частоты.

Дата добавления: 2014-01-20