Необходимо определить средний квартальный коэффициент роста выпуска продукции

Например, имеются следующие данные о выпуске продукции по кварталам отчетного года.

Средняя геометрическая применяется для исчисления среднего коэффициента роста в рядах динамики.

Средние показатели могут рассчитываться по дискретным и интервальным вариационным рядам. При этом расчет производится по средней арифметической взвешенной. Для дискретного ряда данная формула используется так же, как и в приведенном выше примере. В интервальном же ряду для расчета определяются середины интервалов.

В качестве веса в этой задаче был принят показатель общих затрат времени на изготовление всех деталей одним рабочим. Т.к. затраты времени у всех одинаковые, то к аналогичному результату приходим выполняя расчет по формуле средней гармонической простой

Показатель	Кварталы года
I	II	III	IV
Выпуск продукции (в тыс. руб.)
Условные обозначения	y0	y1	y2	y3
Коэффициент роста (снижения) выпуска продукции по сравнению с предыдущим кварталом	-	1.2	1.04	0.976
Условные обозначения		K1=y1/y0	K2=y2/y1	K3=y3/y2

Формула средней геометрической простой применяется для рас­чета среднего коэффициента роста, если промежутки времени, к которым относятся коэффициенты роста, одинаковы.

Средняя арифметическая обладает рядом свойств:

1. Сумма отклонений индивидуальных значений признака от их средней величины равна 0;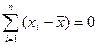

2. От уменьшения (или увеличения) частот каждого значения признака х в n раз величина средней арифметической не изменится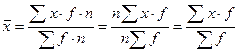

3. Общий множитель индивидуального значения признака может быть вынесен за знак средней:

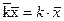
Дата добавления: 2014-01-20