Способы отбора единиц из генеральной совокупности. Основное условие проведения выборочного наблюдения - предупреждение систематических ошибок, возникающих при нарушении принципа равных возможностей попадания в

Основное условие проведения выборочного наблюдения - предупреждение систематических ошибок, возникающих при нарушении принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Выборка может быть:

1) собственно случайная;

2) механическая

3) типическая

4) серийная

5) комбинированная

1. Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного отбора единиц из генеральной совокупности. Это достигается путем присвоения каждой единицы генеральной совокупности порядкового номера, который затем записывается на фишки или шары одинакового размера и формы. Фишки или шары тщательно перемешиваются и отбираются по одной. Можно также использовать таблицы случайных чисел.

Для вычисления средней ошибки выборки используются формулы:

При повторном отборе 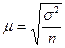; при бесповторном отборе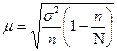

2. При механическом отборе генеральная совокупность разбивается на группы (равные интервалы). При этом величина интервала равна обратной величине доли выборки и из каждой группы отбирается только одна единица (так при 2% выборки отбирается каждая 50-я единица (1:0,02), при 5%, каждая 20-я единица). Чаще всего для избежания систематических ошибок отбираются те единицы, которые находятся в середине группы. Для определения средней ошибки механической выборки используется та же формула, что и при собственно-случайном отборе.

3. При типической выборке генеральная совокупность разбивается на однородные типические группы, а затем из каждой типической группы собственно-случайной или механической выборкой производится отбор единиц в выборочную совокупность. Типическая выборка применяется обычно при изучении сложных статистических совокупностей. Она дает более точные результаты по сравнению с другими способами отбора. Расслоение объектов генеральной совокупности по типически однородным группам может проводиться в соответствии со следующими признаками: территория, отрасль, форма собственности, выручка от реализации продукции (работ, услуг).

При определении ошибки типической выборки находят среднюю из внутригрупповых дисперсий:

а) для доли ;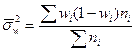

б) для средней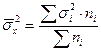

Тогда для определения средней ошибки выборки используются формулы:

а) для доли альтернативного признака при повторном отборе: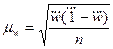

для бесповторного отбора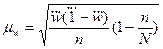

б) для средней величины для повторного отбора ;

для бесповторного отбора

4. Серийная выборка применяется в том случае, если генеральная совокупность разбита на группы еще до начала выборочного обследования.

При серийной выборки из генеральной совокупности отбираются не отдельные единицы, а целые их гнезда (группы). Внутри каждой серии обследуются все без исключения единицы (применяется сплошное наблюдение). Применяется серийные выборки, например, в торговле, где целесообразнее проверить несколько коробок, чем вытаскивать из каждой коробки по пачке. Серийная выборка производится по схеме бесповторного отбора. Для определения средней ошибки выборки применяются формулы:

а) для доли 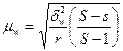, где 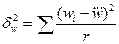- межсирийная дисперсия выборочной доли,

s – число серий в выборке;

S – число серий в генеральной совокупности.

б) для средней 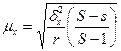где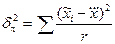

5. Комбинированную выборку применяют в случае, когда отбор единиц из генеральной совокупности представляет собой сложный процесс. Можно, например, комбинировать серийный отбор со случайной выборкой. Пи этом генеральная совокупность разбивается сначала на серии, а затем в каждой серии проводится случайный отбор. Средняя ошибка комбинированной выборки определяется по формулам: при повторном отборе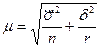

при бесповторном отборе ,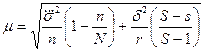

где n – число единиц, взятых в выборку из серий.

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ

Порядок изучения статистической связи. Классификация связей в статистике.

Важная задача статистики состоит в выявлении существующих связей между явлениями. Социально-экономические явления представляют собой результат одновременного воздействия большого числа факторов. При изучении эти явлений необходимо выявить основные факторы и абстрагироваться (не принимать во внимание) от второстепенных.

Рассматривая зависимости между признаками, выделяют две категории связи функциональную и стохастическую.

Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Например, функциональной является зависимость длины окружности или площади круга от радиуса. Модель функциональной связи может быть представлена как Y=f(X). На практике такие связи встречаются в математических формула, а также при расчете сдельной оплаты труда, (если принять за у оплату труда, а за х кол-во изготовленных изделий и учесть, что за каждое изделие оплата 5 руб, то тогда оплата труда выражается зависимостью y=5*x. Такие зависимости называются жестко детерминированными.

В действительности же взаимосвязи в социально-экономических явлениях значительно сложнее, они многофакторные и не носят функционального характера. Поэтому статистикой изучаются стохастические связи. Стохастическая связь- это такая связь между признаками, при которой для каждого значения признака фактора Х признак-результат Y может в определенных пределах принимать любые значения с некоторыми вероятностями, при этом его статистические характеристики (например, среднее значение) изменяется по определенному закону.

Модель стохастической связи может быть представлена в общем виде уравнение Y=f(X, u), где Y-фактическое значение результативного признака;

f(X) –часть результативного признака, сформировавшегося под воздействием фактора X или нескольких факторов X₁, X₂ …X_n;

f(u) - случайная составляющая, часть результативного признака, которая возникла вследствие влияния прочих факторов, а также ошибок измерения признаков.

Частным случаем стохастической связи является корреляционная связь. Это такая связь, при которой с изменением значения признака X закономерно изменяется среднее значение признака Y, в то время как в каждом отдельном случае признак Y с определенной вероятностью может принимать множество различных значений.

Модель корреляционной связи: E(Y/X_1, X₂, … X_m)=f(X_1, X₂, … X_m), Где m – множество факторов, Е - математическое ожидание.

Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению и аналитическому выражению.

По степени тесноты связи различают количественные критерии оценки тесноты связи по шкале Чеддока.

Количественные критерии оценки тесноты связи Таблица 1

Величина коэффициента	Характер связи
До ± 0,3	Практически отсутствует
± 0,3 - ± 0,5	Слабая
± 0,5 - ± 0,7	Умеренная
± 0,7 - ± 1,0	Сильная

Предварительная характеристика направления и тесноты связи между признаками может быть произведена с помощью непараметрических показателей связи: коэффициента Фехнера, коэффициентов корреляции рангов (Спирмена, Кендалла), коэффициента конкордации.

Коэффициент Фехнера Кф оценивает направление и тесноту связи на основе сравнения знаков отклонений значений результативного у и факторного х признаков от их средних арифметических: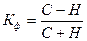

где С — число совпадений знаков отклонений у от и х от 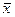по всем единицам изучаемой совокупности; Н — число случаев несовпадений знаков отклонений.

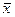Рассчитаем коэффициент Фехнера для рассматриваемого примера. Сравним уровни заработной платы и производительности труда по всем работникам с их средними значениями: = 41280/24 = 1720 руб./чел., = 69600/24 = = 2900 руб./чел. Подсчитаем совпадение знаков отклонений по обоим признакам (табл. 2).

Взаимосвязь уровней производительности труда и заработной платы почтовых работников и расчетные величины для оценки тесноты связи между ними Таблица 2

Номер работ-ника	Производит. труда х, руб. чел.	Заработная плата у, руб.чел.	Знак отклонения от среднего уровня	Совпадения (несовпадение) знаков	Ранги	Разность рангов d	d^2
		Rx	Ry
			-	-	C			-1
			-	-	C
			-	-	C
			-	-	C			-1
			-	-	C			-4
			-	-	C
			-	-	C
			-	-	C	8,5		2,5	6,25
			-	-	C	8,5		0,5	0,25
			-	-	C
			-	-	C
			-	+	Н
			+	-	Н
			+	+	С
			+	+	С			-1
			+	-	Н	16,5		3,5	12,25
			+	+	С	16,5		-0,5	0,25
			+	+	С
			+	+	С	19,5		4,5	20,25
			+	+	С	19,5		-0,5	0,25
			+	+	С
			+	+	С			-1
			+	+	С
			+	+	С
Итого			-	-	-	-	-	-	95,5

Коэффициент Фехнера для нашего примера равен 0,75[(21-3)/24]. Это дает основание считать, что между производительностью труда работников почтовой связи и их заработной платой существует достаточно тесная прямая связь.

Коэффициент корреляции рангов 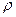(коэффициент Спирмена) учитывает согласованность рангов, т.е. номеров или мест, которые занимают единицы совокупности по каждому из анализируемых признаков, и рассчитывается по формуле:

,

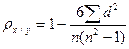где п — количество единиц совокупности; d — разность рангов по признакам х и у.

Порядок сопоставления рангов факторного и результативного показателей таков: единицы совокупности ранжируются по факторному и результативному признакам и каждой единице присваивается номер (место) в упорядоченном ряду признаков. Если встречаются в ряду одинаковые варианты по результативному и факторному признакам, то каждой из них присваивается среднее арифметическое значение их рангов. Коэффициент корреляции рангов может принимать значения от —1 до+1.

В рассматриваемом примере работники почтовой связи ранжированы по возрастанию факторного признака — уровню производительности труда с 1-го по 24-й номер. При ранжировании почтовых работников трижды встретились одинаковые варианты: х = 2550 у работников, занимающих 8-е и 9-е места, х = 3170 у работников, занимающих 16-е и 17-е места, и х = 3600 у работников, занимающих 19-е и 20-е места по возрастанию производительности труда, поэтому им присвоены средние ранги: 8,5; 16,5 и 19,5.

Коэффициент корреляции рангов составил 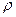=, что подтверждает ранее полученный вывод о положительной тесной связи между признаками.

Достоинством непараметрических показателей связи является возможность их использования при анализе взаимосвязи социально-экономических явлений, не имеющих количественного выражения (атрибутивных признаков, например, зависимости заработной платы от уровня образования; от формы собственности предприятия - государственной, частной, кооперативной.

Для определения тесноты связи между произвольным числом признаков применяют множественный коэффициент ранговой корреляции (коэффициент конкордации):

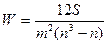, где

m- количество факторов; n-число наблюдений; S-отклонения суммы квадратов суммы рангов по всем факторам от среднего квадрата суммы рангов.

Например, Произведем оценку взаимосвязи между уставным капиталом, количеством и ценой выставляемых на аукцион акций связи. Данные приведены в таблице.

Номер организации	Уставной капитал, х млн. руб.	Число акций у, ед.	Цена акции z, тыс. руб.	Rx	Ry	Rz	Сумма рангов	Квадрат суммы рангов
	310,6		2,3
	245,0		2,1
	147,6		1,9
	185,3		1,8
	420,2		2,5
	570,1		2,6
	263,2		2,4
	80,8		2,2
	127,3		1,6
	346,2		2,0
Итого	-	-	-	-	-	-

S=3333-(165²/10)=3333-2722,5=610,5 W=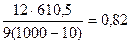

Величина коэффициента конкордации W свидетельствует о весьма тесной связи между размером организации, числом выставляемых акций и их ценой.

Для оценки тесноты связи между двумя признаками исчисляется эмпирическое корреляционное отношени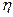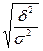е =, где 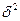-межгрупповая дисперсия; 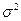-общая дисперсия.

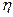²-коэффициент детерминации.

Если коэффициент детерминации >0,7, то связь между признаками достаточно тесная.

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного.

По аналитическому выражению выделяют связи прямолинейные (связь между явлениями приближенно выражена уравнением прямой линии) и нелинейные (криволинейные) (связь выражена уравнением кривой линии: гиперболы, параболы и др.)

Дата добавления: 2014-01-20