Скорость химической реакции

Скорость химической реакции является важнейшей количественной характеристикой динамики химического процесса. Под скоростью гомогенной гомофазной реакции по i-веществу понимают изменение количества i-вещества (в молях, кмолях) в результате химической реакции в единицу времени в единице реакционного объема. Скорость гомогенной гомофазной реакции определяется, как известно, следующим дифференциальным уравнением.

dn_i ┌ моль ┐

r_i = ——— │——— │
Vdτ └л * мин┘

Для реакции общего вида

ν_АА + ν_YY → ν_ВВ + ν_СС

справедливо следующее соотношение

1 1 1 1

—— r_А = —— r_А = —— r_А = —— r_А = r

-ν_А -ν_Y ν_В ν_С

тогда скорость превращения по каждому из веществ составит

dn_i

r_i = ——— = ν_i r

Vdτ

Уравнение, описывающее зависимость скорости химического процесса от концентраций реагирующих веществ, называется кинетическим уравнением. В ряде случаев кинетическое уравнение в общем виде может быть записано как произведение концентраций реагирующих i-веществ в соответствующих степенях (n_i):

r = k

Коэффициент пропорциональности в вышестоящем уравнении называется константой скорости химической реакции (k). Константа скорости реакции численно равна скорости реакции при концентрациях всех реагентов, равных единице, и поэтому ее иногда называют удельной константой скорости реакции. Для сложных по механизму реакций k называют эффективной (наблюдаемой) константой скорости реакции.

Величину n_i принято называть порядком реакции по i-веществу. Сумма порядков по всем реагирующим веществам называется общим порядком реакции.

В элементарных реакциях порядок по i-веществу совпадает со стехиометрическим коэффициентом (n_i = ν_i), а общий порядок реакции, равный сумме стехиометрических коэффициентов реагирующих частиц, называется молекулярностью, которая не может быть больше трех.

Для элементарных реакций выполняется закон действующих масс: скорость простой по механизму химической реакции прямо пропорциональна концентрации реагирующих веществ (действующих масс). При этом, с одной стороны, химическая реакция должна протекать только за счет теплового движения реагентов и без нарушения Максвелл-Больцмановского распределения энергии по степеням свободы реагирующих частиц и, с другой стороны, должен соблюдаться принцип независимости протекания элементарных реакций. Изменение концентраций реагентов не должно заметно менять свойства среды (полярность, вязкость и т.д.).

Кинетические уравнения элементарных реакций имеют следующий вид:

Мономолекулярная реакция

k

А В + D

r = kC_А

Бимолекулярная реакция

k

А + Y В + D

r = kC_АC_Y

k

2А В + D

r = kC²_А

Тримолекулярная реакция

k

А + Y + Z В + D

r = kC_АC_YC_Z

k

2А + Y В + D

r = kC²_АC_Y

В зависимости от порядка или молекулярности реакции размерность константы скорости различна. Константы скорости реакций различных размерностей нельзя сравнивать.

Для гомогенных жидкофазных реакций размерность константы скорости следующая:

Нулевой порядок k

Первый порядок k [τ^‒1]

Второй порядок k

Любой порядок k

Константа скорости реакции, как правило, резко возрастает с ростом температуры.

Зависимость константы скорости реакции от температуры в большинстве случаев может быть описана полуэмпирическим уравнением Аррениуса:

k =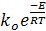

Где,

k_o ‒ предэкспоненциальный множитель;

Е ‒ энергия активации реакции.

Энергия активации элементарной реакции ‒ это энергия, которую необходимо сообщить сверх средней нулевой энергии при данной температуре реагирующим частицам для протекания химической реакции между этими частицами (молекулы, радикалы, ионы и т.п.).

Для сложной по механизму реакции энергия активации лишена физического смысла и называется эффективной (наблюдаемой) энергией активации, отражающей алгебраическую сумму энергий активации отдельных элементарных реакций.

В большинстве случаев, однако, органические реакции являются неэлементарными, т.е. состоящими из некоторой совокупности элементарных стадий, протекающих при участии или с образованием промежуточных частиц (свободные атомы или радикалы, отрицательно или положительно заряженные ионы, ион-радикалы) или комплексов (с катализатором, растворителем и др.). Под элементарной стадией понимают необратимое или обратимое превращение, протекающее через единственное переходное состояние. Совокупность их, т.е. механизм реакции, может быть линейной, разветвленной или замкнутой.

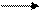а) о о о о о о

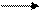
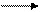
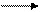
б) о о о о о о

о о о

в) о о о

о о о

Схема линейного (а), замкнутого (б) и разветвленного (В) маршрутов неэлементарных реакций.

Гипотезу о механизме неэлементарных реакций выдвигают на основе имеющихся теоретических представлений и их дальнейшего развития для изучаемой системы. С этой же целью важно привлечь физические и физико-химические методы идентификации промежуточных частиц или комплексов (спектры ЭПР, ЯМР, УФ, ИК и др.) или использовать литературные данные. Необходимое условие правильного составления механизма состоит в том, что при суммировании уравнений всех стадий промежуточные частицы и комплексы должны сокращаться, давая в итоге стехиометрическое уравнение реакции.

Из гипотезы о механизме реакции далее выводят её кинетическое уравнение, имея в виду, что для каждой элементарной стадии верен простой вид уравнения скорости, вытекающей из теории элементарных реакций. Для каждой из элементарных реакций сохраняется и понятие молекулярности, равной числу участвующих в ней кинетически независимых молекул, частиц или комплексов.

Наиболее общий подход к кинетическому описанию процесса состоит в его представлении как системы дифференциальных уравнений для скоростей превращения ключевых веществ данной совокупности элементарных реакций.

Приведем пример разработки уравнения скорости для реакции синтеза метил-третбутилового эфира (МТБЭ) при взаимодействии изобутилена с метанолом при повышенной температуре в присутствии кислотного катализатора.

СН₃ t, Н⁺ СН₃

СН₃‒С=СН₂ + СН₃ОН СН₃‒С‒ОСН₃

СН₃

Данная реакция протекает по двум элементарным стадиям. На первой стадии изобутилен взаимодействует с сольватированным протоном кислотного катализатора с образованием соответствующего карбокатиона.

СН₃ k₁ СН₃

СН₃‒С=СН₂ + Н⁺ СН₃‒С+

k_-1 СН₃

На второй элементарной стадии карбокатион реагирует с метанолам, образуя метил-третбутиловый эфир и восстанавливая катализатор.

СН₃ k₂ СН₃

СН₃‒С+ + СН₃ОН СН₃‒С‒ОСН₃ + Н⁺

СН₃ СН₃

Из первого стехиометрического уравнения реакции синтеза МТБЭ видно, что скорость образования эфира равна скорости расходования изобутилена. Поскольку эфир образуется на второй стадии, то по закону действующих масс скорость реакции можно записать следующим образом.

r = 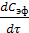= ‒ = 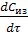k₂*[KK]*С_мет (3.1)

В последнее уравнение входит концентрация карбокатиона, которую трудно определить обычными методами. В действительности при большинстве неэлементарных реакций по промежуточным комплексам или частицам устанавливается так называемый квазистационарный режим. Он характеризуется тем, что скорость изменения их концентраций (d[КК]/dτ) пренебрижимо мала по сравнению со скоростью самой химической реакции (dС_эф/dτ, ‒dС_из/dτ), иначе, время жизни активных частиц или комплексов ничтожно по сравнению с длительностью реакции. В этом случае производные d[КК]/dτ можно приравнять нулю, найти из полученного алгебраического уравнения квазистационарную концентрацию карбокатиона и подставить её в кинетическое уравнение реакции.

Такой способ построения кинетических уравнений неэлементарных реакций, предложенный Боденштейном и развитый Н.Н.Семеновым, называется методом стационарных концентраций (принцип стационарности Боденштейна-Семенова). Он позволяет исключить из кинетического описания процесса неизвестные концентрации промежуточных комплексов или частиц и получить одно или некоторый минимум дифференциальных уравнений скорости.

В нашем случае карбокатион образуется по первой прямой элементарной реакции и расходуется по первой обратной элементарной реакции и по второй элементарной реакции. Скорость образования карбокатиона, которая равна нулю, можно записать в следующем виде.

d[КК]/dτ = k₁*C_из*С_кат ‒ k_-1*[КК] ‒ k₂*[КК]*С_мет = 0 (3.2)

Из уравнения (3.2) найдем.

k₁*C_из*С_кат

[КК] = —―———— (3.3)

k_-1 + k₂*С_мет

Подставим полученное выражение для концентрации карбокатиона в уравнение скорости реакции (3.1) и получим

k₂*k₁*C_из*С_кат*С_мет

r = 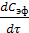= ‒ = 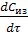k₂*[KK]*С_мет = —―——————— (3.4)

k_-1 + k₂*С_мет

Проанализируем полученное уравнение скорости. Может быть два основных случая.

1. Первая стадия является лимитирующей, т.е. её скорость очень мала и тогда можем пренебречь значением k_-1 в знаменателе. Уравнение скорости реакции после проведения сокращений примет следующий вид.

r = 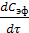= ‒ = 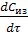k₁*C_из*С_кат (3.5)

Скорость реакции равна скорости первой лимитирующей стадии.

2. Вторая стадия является лимитирующей, т.е. её скорость очень мала и тогда можем пренебречь значением k₂*С_мет в знаменателе. Уравнение скорости реакции примет следующий вид.

k₂*k₁*C_из*С_кат*С_мет

r = 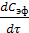= ‒ = 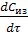—―——————— = k_наб*C_из*С_кат*С_мет (3.6)

k_-1

Какое кинетическое уравнение из полученных (3.4) или (3.5) или (3.6) является истинным показывает кинетическое исследование данной реакции.

Дата добавления: 2014-01-20