Введение в предмет ЭПУ

Смоленск 2005

По курсу

КОНСПЕКТ ЛЕКЦИЙ

М.А. Амелина

Филиал в г. Смоленске

e-mail: [e-mail]

Кафедра промышленной электроники

Факультет компьютерных технологий и электроники

«Электронные промышленные устройства»

(7 семестр)

Электронные промышленные устройства (ЭПУ)

Литература

1. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники. М., Энергия, 1972, 512 с. 621.391 /075.8 /Т32

2. Электронные промышленные устройства. Учебник. Васильев В.И., Гусев Ю.М., Миронов В.Н., Обухов С.Г., Семеран В.А. М.: Высш. школа, 1980. - 303 с.

3. С.И. Баскаков Радиотехнические цепи и сигналы: Учеб. для вузов. – 3-е изд-е, перераб. и доп. – М.: Высш. шк., 2000. – 462 с.: ил.

4. А.Б. Сергиенко Цифровая обработка сигналов: Учебник для вузов – СПб.: Питер, 2002– 608 с.: ил.

5. Ю.Г. Карпов Теория автоматов: Учебник для вузов – СПб.: Питер, 2002 – 224 с.: ил.

6. Прянишников В.А. Электроника: Курс лекций. — 2-е изд. исп и под. — СПб.: КОРОНА принт, 2000. — 416 с., ил.

7. Микросхемы для аналого-цифрового преобразования и средств мультимедиа. Вып. 1 /Серия «Интегральные микросхемы». М. Додэка 1996 г., 384 с. 681.3(083) И 73.

8. Федорков Б.Г., Телец В.А. Микросхемы ЦАП и АЦП: Функционирование, параметры, применение. – М.: Энергоатомиздат, 1990. – 320 с.: ил.

9. Шкритек П. Справочное руководство по звуковой схемотехнике: Пер. с нем. – М.: Мир, 1991. – 446 с.: ил.

10. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем. – М.: Мир, 1982. – 512 с., ил.

Электронными промышленными устройствами называют функционально и конструктивно законченные средства получения, обработки, использования информации для управления объектами и процессами, а также отображения состояния объекта и связи его с другими управляющими средствами.

Вначале устройства выполняли функции измерения и регистрации, по мере совершенствования элементной базы и повышения ее надежности область применения стала включать в себя автоматизированные (с участием человека) и полностью автоматические управляющие системы. Одна из первых и важнейших задач управления – регулирование состояния объектов. Регулирование требует последовательности выполнения операций, основными из которых являются:

1) получение сведений о состоянии объекта или процесса;

2) получение извне командных воздействий, определяющих требуемое состояние объекта или процесса;

3) обработка полученных сигналов с целью наиболее эффективного приведения объекта в соответствие с заданием;

4) формирование управляющих воздействий, которые с помощью исполнительных органов изменяют режим работы объекта.

За последние годы способы управления, аппаратура и подход разработчика к созданию автоматов существенно изменились, что связано с цифровым представлением информации и программной реализацией алгоритмов. Это стало возможным благодаря интенсивному развитию микроэлектроники, приведшему к увеличению количества электронных компонентов на единицу площади кристалла. Что, в свою очередь, позволило разместить вычислитель плюс контроллер (микро-ЭВМ) на одном кристалле полупроводника, заключенном в единый корпус. Такая интегральная схема и называется микропроцессором. Основные изменения в проектировании ЭПУ состоят в следующем:

1) наиболее существенные операции над сигналами производятся после представления их в форме двоичных многоразрядных чисел;

2) вместо линейных преобразований над аналоговыми (непрерывными во времени) сигналами стали использоваться конечно-разностные преобразования (цифровое управление);

3) произошла централизация функций: вместо нескольких управляющих устройств для сложного объекта может использоваться один процессор, поочередно выполняющий их функции в режиме разделения времени;

4) вследствие этого усилилось внимание к алгоритмической стороне управления (т.е. к написанию эффективного и надежного программного обеспечения)

5) Усилилось внимание к созданию встроенных средств самодиагностики устройств.

Курс ЭПУ состоит из двух частей. В первой части (читаемой в 7 -ом семестре) будут рассмотрены:

· информационные основы построения ЭПУ: количественные меры информации, разновидности сигналов, методы модуляции, квантование сигналов по времени и по уровню, теорема отсчетов (Котельникова, Найквиста);

· основные разновидности цифро-аналоговых (ЦАП) и аналого-цифровых (АЦП) преобразователей;

· основы цифровой обработки сигналов с помощью ЦАП, АЦП и цифровых фильтров.

Во второй части курса (читаемой в 8-ом семестре) будут рассмотрены:

· Цифровые интегральные схемы (малой, средней большой степени интеграции), их применение для синтеза комбинационных и последовательностных логических устройств;

· Методы синтеза цифровых автоматов;

· Моделирование цифровых устройств с помощью программы MICROCAP-7.

В 8-ом семестре запланирован типовой расчет, в котором студенты должны самостоятельно разработать цифровое устройство и промоделировать его функционирование в различных режимах с помощью программы MICROCAP-7(8).

1. Информационные основы построения электронных промышленных устройств (ЭПУ)

1.1. Сигналы в электронных промышленных устройствах

1.1.1. Задачи, решаемые в процессе проектирования ЭПУ

На начальной стадии проектирования ЭПУ обычно решаются задачи сбора и первичной обработки информации. Полезная информация об управляемом процессе содержится в первичных сигналах датчиков. Эти сигналы, как правило, искажены помехами и ошибками измерения. Основные задачи первичной обработки сигналов:

1) вычисление и преобразование спектров сигналов, например, для правильного выбора характеристик квантования аналоговых сигналов (частота и число уровней квантования);

2) нормализация, усиление или ослабление сигналов.

3) предварительная цифровая или аналоговая фильтрация сигналов с целью выделения из них полезной составляющей, используемой на последующих этапах обработки;

4) квантование аналоговых сигналов по времени и уровню;

На последующих стадиях проектирования решаются задачи измерения и обработки информации об управляемом процессе. Можно выделить следующие типичные задачи:

1) определение текущих параметров измеряемых процессов (например, скоростей и ускорений их протекания);

2) прогнозирование хода управляемых процессов, кодирование;

3) цифроаналоговые преобразования и т. д.

Таким образом, электронные устройства управления и контроля связаны с преобразованием и обработкой информации.

Информацией называется совокупность каких-либо сведений об изучаемом процессе (объекте), являющаяся объектом передачи, распределения, преобразования, хранения или непосредственного использования. Информация в процессе взаимодействия с ЭПУ с целью управления некоторым объектом проходит несколько фаз. Рассмотрим основные из них (рис. 1.1).

Восприятие состоит в том, что формируется образ объекта, производятся его опознание и оценка. При восприятии нужно отделить полезную информацию от шумов, что в некоторых случаях (тонкие биологические, физико-химические эксперименты; сложные производственные условия; радиосвязь, локация, астрономия и др.) связано со значительными трудностями. В результате восприятия получается сигнал в форме, удобной для передачи или обработки. В фазу восприятия могут включаться операции подготовки информации, ее нормализации, квантования, кодирования, модуляции сигналов и построения моделей.

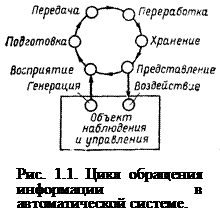Передача информации состоит в переносе ее на расстояние посредством сигналов различной физической природы соответственно по механическим, гидравлическим, пневматическим, акустическим, оптическим, электрическим или электромагнитным каналам. Прием информации на другой стороне канала имеет характер вторичного восприятия со свойственными ему операциями борьбы с шумами.

Обработка информации заключается в решении задач, связанных c преобразованием информации, независимо от их функционального назначения. Применение ЭВМ обобщает и централизует функции обработки, имеющие отношение главным образом к моделям ситуации и принятию решений при управлении. Обработка производится при помощи устройств или машин, осуществляющих аналоговые или цифровые преобразования поступающих величин и функций. Промежуточным этапом обработки может быть хранение в запоминающих устройствах. Извлечение информации из запоминающих устройств также имеет характер восприятия и связано с борьбой с помехами.

Представление (или отображение) информации требуется тогда, когда в цикле обращения информации принимает участие человек. Оно заключается в демонстрации перед человеком условных изображений, содержащих качественные и количественные характеристики выходной информации. Для этого используются устройства, способные воздействовать на органы чувств человека.

Из устройства обработки информация может выводиться не только оператору, но и непосредственно воздействовать на объект управления.

Воздействие состоит в том, что сигналы, несущие информацию, производят регулирующие или защитные действия, вызывая изменения в самом объекте.

Не все информационные системы замкнуты. Существуют и разомкнутые системы, в которых информация передается от источника к приемнику или потребителю. Активное воздействие на отбираемую от источника информацию может оказывать либо сам источник, либо потребитель. Часть системы, оказывающую активное воздействие на ее работу, называют субъектом, а пассивную — объектом.

Как объектом, так и субъектом может быть человек Ч или машина М. Возможные отношения между ними в разомкнутой информационной системе приведены на рис. 1.2.

Объект как источник информации неисчерпаем. Но подавляющая часть потоков отображения его состоянии рассеивается и только небольшая часть, отвечающая потребности и определяемая принятым в информационной системе языком, ответвляется к приемнику в виде параметров наблюдения Х или управления Y.

1.1.2. Виды информации

Общее философское понятие информации – это отражение реального мира. По структуре и метрическим свойствам информация подразделяется на параметрическую и топологическую.

Топологическая – геометрические образы, карты местности, различные плоские изображения и объемные объекты. В инженерной практике широкое распространение имеет параметрическая информация (наборы численных оценок каких-либо параметров – измеряемых величин), которую можно свести к следующим четырем основным видам: событию, величине, функции и комплексу.

Событие

Первичным и неделимым элементом информации является элементарное двоичное событие А (рис. 1.3, а) — выбор из утверждения или отрицания, истины или лжи, согласия или несогласия, наличия или отсутствия какого-либо явления. Примером могут служить сведения об импульсе или паузе в электрической цепи, выпуске годного или негодного изделия, достижении или недостижении измеряемой величиной одного определенного значения, черном или белом элементах телевизионного изображения, попадании или непопадании в цель, наличии или отсутствии команды и т. д.

Двоичность (есть или нет) события позволяет представлять его условно в геометрической символике точкой и пробелом (• и О), в арифметической символике – единицей и нулем (1 и 0), в сигнальной символике – импульсом и паузой (_éù_. и __).

Событие является категорией нулевой меры, т. е. не имеет геометрических измерений. Поэтому оно и представимо точкой.

Величина

Величина Х (рис. 1.3, б) есть упорядоченное в одном измерении (по шкале значений) множество событий, причем каждое из них отвечает принятию величиной какого-либо одного значения. Величина может быть или дискретной, или непрерывной; в первом случае множество событий счетно, во втором — несчетно. Геометрически величину можно представить линией (рис. 1.3, б).

Функция

Функция Х(Т) (рис. 1.3, в), X(N) или X₂(X₁) есть соотношение между величиной и временем, пространством или другой величиной. В этом смысле функцию можно трактовать как двумерное поле событий.

Комплекс

Полный комплекс информации X(T,N) (рис 1.3, г) есть соответствие между величиной, с одной стороны, и временем и пространством – с другой. Таким образом, полный комплекс информации есть трехмерное поле событий.

Следовательно, источник информации обладает способностью изменять во времени или пространстве свое состояние. Источником информации могут быть различные физические величины и процессы, например: ЭДС термопары (величина), ток фотодиода (фототранзистора) (событие, величина, функция), напряжение тензодатчика, горение сигнальной лампы (событие) и т. д. Сведения о состоянии источника называются сообщениями. Для их передачи используются сигналы, которые по имеющимся каналам поступают к приемнику сообщения.

Таким образом, сигналом называется физический процесс, параметры которого содержат информацию (сообщение) и который пригоден для обработки и передачи на расстояние.

Одно и то же сообщение может быть передано разными сигналами (например, жест регулировщика и сигнал светофора). Сигнал может быть электрическим, акустическим, оптическим и др. — в зависимости от свойств источника, приемника и среды, в которой передается сообщение. Основное внимание будем уделять электрическим сигналам (телевидение, радио, телефония), хотя все чаще применяются устройства, в которых сообщения передаются некоторым набором сигналов, например, в оптроне электрический сигнал на входе превращается в световое излучение, которое затем подвергается обратному преобразованию. При всех преобразованиях сигнала сохраняется содержащаяся в нем информация, хотя некоторые потери ее возможны (искажения, появление шумов и других видов помех).

Так как сообщение предполагает изменение состояния источника, сигнал также должен иметь какой-то один или группу параметров, подвергающихся изменению, модуляции. Сигнал, в котором ничего не меняется, не может нести информации. Показания прибора становятся информативными только при их изменении, подобно тому как, сейсмограф привлекает внимание лишь тогда, когда он после длительной паузы свидетельствует о толчке.

В зависимости от того, какой исходной (априорной) информацией о свойствах источника и характере протекания сигнала во времени располагаем, принято разделять сигналы на детерминированные и случайные. Детерминированными считаются такие сигналы, поведение которых можно предсказать заранее с приемлемой точностью. Допустим, что генератор вырабатывает синусоидальное напряжение с амплитудой U₀, частотой w₀ и начальной фазой j₀. Мгновенное значение напряжения на выходе генератора в любой момент времени: u(t)=U₀cos((w₀t + j₀). Таким образом, детерминированный сигнал может быть задан своей математической моделью — описанием в виде некоторой, вполне определенной функции времени, что облегчает анализ различных свойств сигнала и способов его преобразования.

Случайными называют сигналы, которые, в отличие от детерминированных, нельзя предсказать с достаточно малой погрешностью, так как состояние источника информации в данном случае определяется большим числом факторов, поэтому каждая серия измерений описывается своей функцией времени (реализацией процесса). Классическим примером случайных сигналов являются помехи – наводки по цепям электропитания, шумы усилителей, сбои в работе цифровой аппаратуры. В более широком смысле любой сигнал, точный закон изменения которого неизвестен, рассматривается как случайный. Для описания случайных сигналов используются вероятностные (стохастические) законы, характеризующие распределение вероятностей отдельных значений сигнала для каждого момента времени.

1.1.3. Преобразование Фурье. Спектры сигналов

Представление сигнала во временной области позволяет определить его параметры, энергию, мощность и длительность. Существуют также формы математического описания, лучше отображающие другие параметры. Нередко уделяется большое внимание изучению частотных свойств сигнала. Для этого используется представление сигнала в частотной области в виде спектра, получаемого на основе математического аппарата преобразования Фурье. Знание частотных свойств позволяет решать задачи идентификации характеристик сигнала (определения его наиболее информативных параметров), фильтрации (выделения полезного сигнала на фоне помех), выбора частоты дискретизации непрерывного сигнала. Одним из важнейших параметров сигнала является ширина его частотного спектра, так как именно этот параметр оказывается определяющим при согласовании сигнала с аппаратурой обработки и передачи информации. Полагая, что сигнал описывается известной функцией времени, т. е. является детерминированным, рассмотрим особенности получения и анализа частотных спектров.

Пусть исследуемый сигнал описывается периодической функцией времени x(t), которая удовлетворяет условиям Дирихле, т. е. является кусочно-непрерывной и кусочно-монотонной в пределах периода ее изменения Т, а в точках разрыва принимает ограниченные значения. Тогда функцию x(t) можно представить в виде ряда Фурье:

коэффициенты которого определяются по формулам:

Физически такое представление сигнала соответствует выделению постоянной составляющей a₀, первой гармоники с частотой w₁ =2 p / T и высших гармоник с частотами 2 w₁, 3 w₁ и т.д. Распространена и другая форма записи ряда Фурье:

Где постоянную составляющую a₀, амплитуду a_k и фазу j_k k-ой гармоники сигнала находят как:

Совокупность значений a_k и j_k (k =1, 2, 3,…) называют амплитудным и фазовым частотными спектрами сигнала (спектром амплитуд и спектром фаз), а последовательность операций по нахождению указанных коэффициентов для каждой гармоники сигнала – гармоническим анализом.

Часто удобно использовать ряд Фурье в комплексной форме, выражение для которого несложно выводится при использовании для гармонических функций вещественного аргумента формул Эйлера :

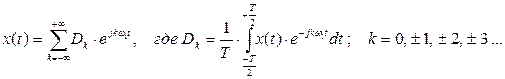
Используя разложение периодической функции x(t) в ряд Фурье, а также свойство ортогональности составляющих его гармонических функций, несложно показать, что средняя за период мощность периодического сигнала при единичном сопротивлении нагрузки определяется соотношением:

Таким образом, средняя мощность сигнала определяется только его спектром амплитуд и не зависит от спектра фаз. Из последнего соотношения (равенство Парсеваля для периодического сигнала) следует, что независимо от формы сигнала если его разложение в ряд Фурье существует, то амплитуда гармоники падает с ростом ее частоты (поскольку мощность конечна).

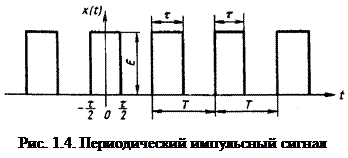
Рассмотрим частотный спектр периодического импульсного сигнала (рис. 1.4). Пользуясь предыдущими соотношениями несложно получить выражения для амплитудного частотного спектра:

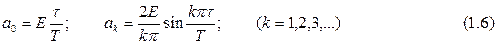
который удобно представить графически в виде отрезков длины a_k, проведенных перпендикулярно оси, на которой наносятся значения частот kw₁.

На рис. 1.5 приведен график амплитудного частотного спектра исследуемого сигнала для t/T = 1/2 (по оси ординат отложены относительные значения амплитуд гармоник a_k/E). Как видно из графика, в спектре сигнала преобладают низкочастотные составляющие. Воспользовавшись формулой (1.5), нетрудно убедиться, что распределение средней мощности сигнала по его гармоникам является следующим: 50%-постоянная составляющая, 40% — первая гармоника, 5% - третья гармоника, 1% - пятая гармоника и т.д. Таким образом, в диапазоне частот (0...2 w₁) содержится 90 % средней мощности импульсного сигнала, в полосе частот (0…4 w₁) – 95 % мощности сигнала.

Изменение соотношения между длительностью t и периодом Т следования импульсов приводит к перераспределению указанной мощности сигнала по отдельным участкам спектра — уменьшается удельный вес его низкочастотных составляющих, возрастает удельный вес высших гармоник. На рис. 1.6 показан график амплитудного частотного спектра для t / Т = 1/5. Вычисления показывают, что 90 % средней мощности сигнала содержится в диапазоне частот (0 … 5 w₁, а 95 % — в полосе (0 … 10 w₁). Оценивая практическую (эффективную) ширину частотного спектра D w по 90%-ному содержанию мощности, можно воспользоваться следующей формулой (см. рис. 1.5 и рис. 1.6):

откуда видно, что D w определяется главным образом длительностью прямоугольного импульса t.

Частотный спектр непериодического сигнала формально можно получить из спектра соответствующего периодического сигнала, принимая Т®¥ в формулах (1.1). В этом случае разность частот между двумя соседними гармониками w₁ = 2p / T стремится к нулю, т. е. частотный спектр из дискретного (линейчатого) становится непрерывным (сплошным). Если функция x(t), описывающая исследуемый сигнал, на любом конечном интервале удовлетворяет условиям Дирихле и, кроме того, является абсолютно интегрируемой на бесконечном промежутке (-¥, +¥), т. е.

то частотный спектр этой функции определяется интегралом Фурье (или прямым преобразованием Фурье):

Для выяснения физического смысла прямого преобразования Фурье (1.8) приведем формулу обратного преобразования Фурье, осуществляющего обратный переход от изображения Х(jw) к оригиналу — временной функции х(t):

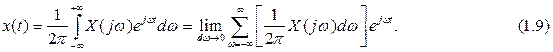
Отсюда видно, что интеграл Фурье позволяет представить непериодическую функцию x(t) в виде суммы бесконечного числа гармоник с бесконечно малыми амплитудами DА(jw) = (1/2p)Х(jw)Dw и с частотами, занимающими диапазон от –¥ до +¥. Таким образом, изображение Х(jw) характеризует плотность распределения амплитуд гармонических составляющих по отдельным участкам спектра и поэтому нередко называется спектральной плотностью сигнала. Полученное изображение

где Х(w) = | X(jw) | — амплитудный частотный спектр; q(w) = arg X(jw) — фазовый частотный спектр сигнала (тэта).

При определении энергии сигнала x(t) можно воспользоваться равенством Парсеваля

В левой части равенства записано выражение для полной энергии сигнала W во временной области, в правой — та же энергия, но подсчитанная в частотной области, с учетом характера распределения амплитудного частотного спектра.

Найдем частотный спектр одиночного прямоугольного импульса, принимающего значение Е на интервале [-t /2,t /2].

Используя (1.8) несложно получить

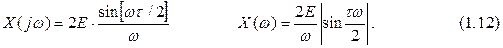
Как видно из рис. 1.7, энергия исследуемого сигнала также в основном сосредоточена в области низких частот (90% полной энергии сигнала содержится в диапазоне частот от 0 до w=2p /t, 95%—в диапазоне частот, не превышающих w = 4p /t). Таким образом, как и в случае периодического импульсного сигнала (см. рис. 1.4), здесь можно говорить о практической ширине частотного спектра D w, которая влияет на поведение (форму) сигнала.

Если принять, что полоса частот D w содержит 90% энергии сигнала, то получаем D f =D w /2 p = 1/ t. Иногда последнее выражение записывают так

t Df = 1 (1.13)

и называют его соотношением неопределенностей. Как видно из (1.13), чем короче импульс (меньше t), тем более широкий спектр должен быть сохранен при передаче сигнала, например, по линии связи. Удлинение импульса позволяет обойтись узкополосной линией связи для передачи значительной части энергии сигнала. Для рассмотренного ранее периодического импульсного сигнала полоса частот D w, подсчитываемая по 90%-ному содержанию мощности, также принимает значение, равное 2 p /t.

1.1.4. Носители сигналов и их модуляция

Итак, назначение сигналов заключается в том, чтобы с помощью параметров какого либо физического процесса отобразить информацию (а именно события, величины, функции).

Преобразование сигнала, заключающееся в изменении какого-либо его информативного параметра в соответствии с передаваемым сообщением, называется модуляцией. Чаще всего для этих целей используется изменение параметров колебаний или импульсных последовательностей. Обратные операции восстановления величин, вызвавших изменение параметров при модуляции, называются демодуляцией.

Для образования сигналов используются фиксированный уровень (рис. 1.8, а), колебания (рис. 1.8, б) или импульсы (рис. 1.8, в) любой физической природы, которые рассматриваются как носители информации. В исходном состоянии эти носители представляют собой как бы чистую поверхность, подготовленную к нанесению необходимых данных — модуляции. Последняя заключается в том, что изменяется какой-либо один или несколько (сложная модуляция) параметров носителя в соответствии с передаваемой информацией. Эти параметры будем называть информационными.

Если обозначить параметры носителя через a₁,a₂..., a_n, то носитель как функция времени может быть представлен в виде

U_Н=g(a₁,a₂..., a_n,t)

Модулированный носитель (сигнал) можно описать в виде

U_X=g(a₁,…, a_i+Da_i(t),…, a_n, t)

где Da_i(t) —переменная составляющая параметра носителя, несущая информацию, или модулирующая функция. Последняя обычно связана с информационной (управляющей) функцией х линейной зависимостью

Da_i=Кх,

где К— коэффициент пропорциональности.

Первый тип носителя Uн(t) —постоянное состояние (рис. 1.8, а), например, постоянное напряжение имеет только один информационный параметр; это в данном случае—значение напряжения, причем модуляция сводится к такому изменению напряжения, чтобы оно в определенном масштабе представляло передаваемые данные. При этом может изменяться и полярность напряжения.

Второй тип носителя—колебание (рис. 1.8, б), например, переменное напряжение содержит три таких параметра: амплитуду U, фазу j, частоту w (или период T=2p /w).

Третий тип носителя—последовательность импульсов (рис. 1.8, в) предоставляет еще большие возможности. Здесь параметрами модуляции могут быть: амплитуда импульсов U, фаза импульсов j, частота импульсов f, длительность импульсов или пауз t, число импульсов n и комбинация импульсов и пауз, определяющая код k. В последнем случае имеет место так называемая кодо-импульсная модуляция.

Ниже приводится перечень основных видов модуляции для носителей перечисленных типов с их названиями и обозначениями.

Носитель первого типа (рис. 1.8, а)

ПМ—прямая модуляция.

П р и м е ч а н и е. Изменение постоянного напряжения или тока избегают называть модуляцией, хотя последняя (от латинского modulatio — мерность) характеризует придание размера вообще.

Носитель второго типа (рис. 1.8, б)

AM—амплитудная модуляция (AM—amplitude modulation);

ЧМ—частотная модуляция (FM—frequency modulation);

ФМ—фазовая модуляция (РМ—phase modulation).

П р и м е ч а н и е. Частотную и фазовую модуляцию иногда называют угловой модуляцией.

Носитель третьего типа (рис. 1.8, в)

АИМ—амплитудно-импульсная модуляция (РАМ— pulse-amplitude modulation);

ЧИМ—частотно-импульсная модуляция (PFM— pulse-frequency modulation);

ВИМ—время-импульсная модуляция (РТМ—pulse-time modulation);

ШИМ—широтно-импульсная модуляция (PDM— pulse-duration modulation);

ФИМ—фазо-импульсная модуляция (РРМ—pulse-phase modulation);

СИМ—счетно-импульсная модуляция (PNM—pulse-number modulation);

КИМ—кодо-импульсная модуляция (РСМ—pulse-code modulation).

П р и м е ч а н и я:

1) ШИМ и ФИМ являются частными случаями ВИМ.

2) Строго говоря, КИМ нельзя рассматривать как отдельный вид модуляции, хотя этот термин и получил широкое распространение; при КИМ используется любой вид модуляции носителя, параметры которого отображают кодовые величины.

3) Счетно-импульсная модуляция (СИМ) является частным случаем КИМ: информация передается числом импульсов.

Типичные сигналы, различающиеся видами модуляции, показаны на рис. 1.9 для случая равномерного возрастания отображаемой величины х(t). Как видно, счетно-импульсная (СИМ) и кодо-импульсная модуляции (КИМ) связаны с квантованием по уровню непрерывной величины х: АИМ, ЧИМ, ВИМ, СИМ и КИМ неизбежно приводят к дискретности отсчетов во времени. Другие виды модуляции принципиально сохраняют непрерывную структуру информации.

Амплитудно-импульсная модуляция имеет две разновидности: АИМ-1, при которой верхние участки импульсов (амплитуды) повторяют форму модулирующей функции (огибающей); АИМ-2, при которой амплитуда в пределах элементарного импульса остается неизменной, определяемой значением модулирующей функции в начале импульса (рис. 1.10).

Время-импульсная модуляция выполняется в нескольких вариантах, дополнительно представленных на рис. 1.11. Информационным параметром сигналов ШИМ служит ширина импульсов или пауз, а сигналов ФИМ — расстояние между первым (опорным) и вторым (информационным) импульсами каждого периода. Следует обратить внимание на отличительные особенности симметричной модуляции ШИМ-С и ациклических—ШИМ-А и ФИМ-А. Последние наиболее экономичны, так как в них практически отсутствуют неиспользуемые промежутки времени. Значащие интервалы вплотную прилегают один к другому, а короткие импульсы или паузы размечают границы.

Все импульсные сигналы могут иметь высокочастотное заполнение — сигнал несущей частоты. Чтобы подчеркнуть это обстоятельство, применяют двойные обозначения видов модуляции, например АИМ-ЧМ, КИМ-ЧМ и т. д., где второй вид модуляции относится к сигналам несущей частоты.

1.2. Дискретизация сигналов

В процессе взаимодействия аналоговых и цифровых систем обработки информации можно наблюдать следующие формы представления сигналов:

1) непрерывное время — непрерывная величина;

2) дискретное время — непрерывная величина;

3) непрерывное время — дискретная величина;

4) дискретное время — дискретная величина.

Первая форма соответствует непрерывным (аналоговым) сигналам, четвертая — цифровым. Две другие формы являются промежуточными.

Процедура аналого-цифрового преобразования непрерывных сигналов, которую реализуют с помощью АЦП, представляет собой преобразование непрерывной функции U(t), описывающей исходный сигнал, в последовательность чисел {U(t_n)}, n = 0, 1, 2,..., отнесенных к некоторым фиксированным моментам времени. В большинстве случаев эту процедуру можно разделить на две самостоятельные операции. Первая из них называется дискретизацией (дискретизацией по времени) и состоит в преобразовании непрерывной функции U(t) в непрерывную последовательность {U(t_n)}, что соответствует переходу из формы 1 в форму 2. Вторая называется квантованием (дискретизацией по уровню) и состоит в преобразовании непрерывной последовательности в дискретную {U(tn)}, что соответствует переходу из формы 2 в форму 4.

В последнее время все чаще предпочитают производить обработку сигнала не в аналоговой, а в цифровой форме. Обработка и передача дискретной (цифровой) информации имеет ряд преимуществ по сравнению с информацией, заданной в непрерывном виде (аналоговой). Дискретные сигналы в меньшей степени подвержены искажениям в процессе передачи и хранения, они легко преобразуются в двоичный цифровой код и обрабатываются с помощью цифровых вычислительных устройств. Преимущество цифровой обработки заключается как в обеспечении большей точности и воспроизводимости результатов, так и в меньшей чувствительности к помехам. Недостатком является большая сложность схемы, однако значение этого фактора по мере возрастания степени интеграции цифровых схем убывает.

1.2.1. Дискретизация непрерывных сигналов по времени

При использовании цифровой обработки сигнала (ЦОС) вместо непрерывной величины обрабатывается дискретная цифровая последовательность. При переходе от аналоговой формы представления информации к цифровой необходимо в первую очередь решить вопрос:

Как без потери информации представить непрерывное входное напряжение числовой последовательностью в виде отдельных отсчетов (дискрет)?

В основе дискретизации непрерывных сигналов лежит принципиальная возможность представления их в виде взвешенных сумм

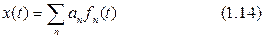
где а_п — некоторые коэффициенты или отсчеты, характеризующие исходный сигнал в дискретные моменты времени; f_n(t) — набор элементарных функций, используемых для восстановлении сигнала по его отсчетам (рис. 1.12).

Многочисленные системы дискретного представления непрерывных сигналов можно разделить на системы, использующие постоянный период дискретизации (равномерная дискретизация) и переменный (адаптивная дискретизация).

Наиболее распространенной формой дискретизации является равномерная, в основе которой лежит теорема отсчетов (или теорема Котельникова–Найквиста):

Всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящими друг от друга на интервалы времени не более Dt=1/2F_max, где F_max – максимальная частота в спектре сигнала.

Согласно этой теореме, в качестве коэффициентов а_n необходимо использовать мгновенные значения сигнала x(t_n) в дискретные моменты времени t_n = nDt, а период дискретизации выбирать из условия

Dt £ 1/2F_max (1.15)

где F_m — максимальная частота спектра исходного сигнала.

Дата добавления: 2014-01-20