Метод зон Френеля. Принцип Гюйгенса-Френеля

Принцип Гюйгенса-Френеля

Световая волна, возбуждаемая каким-либо источником света, может быть представлена как результат суперпозиции когерентных вторичных волн, «излуча­емых» фиктивными источниками.

Дифракционные явления присущи всем волновым процессам, но особенно отчетливо проявляются лишь в тех случаях, когда длины волн излучений сопоставимы с размерами препятствий. Так, звуко­вые волны хорошо слышны за углом дома, т.е. звуковая волна его огибает. Для наблюдения же дифракции световых волн необходимо создание специальных условий. Это обусловлено малостью длин све­товых волн (λ < 1 мкм).

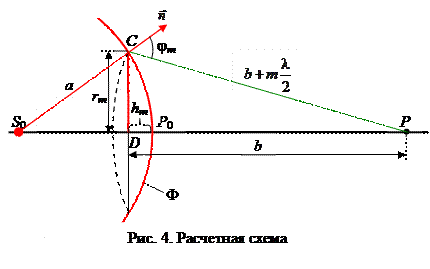
Метод Френеля объясняет прямолинейность распространения света в свобод­ной от препятствий однородной среде. Чтобы показать это, рассмот­рим действие сферической световой волны от точечного источника S ₀ в произвольной точке пространства Р.

Волновая поверх­ность Ф разбивается на зоны так, чтобы расстояния от краев зоны до точки наблюдения Р отличались на l/2:

Р ₀ Р-Р ₁ Р-Р ₂ Р-…= l/2,

тогда колебания в точку Р приходят в противофазе, и амплитуда результирую­ще­го колебания:

А = А ₁ - А ₂ + А ₃ - А ₄ + … ± А_m (1)

Амплитуды коле­ба­ний оценим по площадям зон Френеля. Площадь m -й зоны Френеля:

, (2)

где

(3)

- площадь одного сегмента.

Из D S ₀ CD и D РCD:

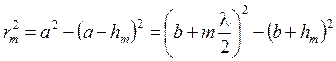
(4)

.

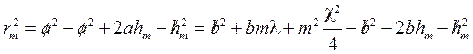
Площадь m -й зоны Френеля:

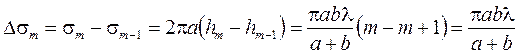(5)

не зависит от номера зоны m, следовательно, площади всех зон Френеля одинаковы. Вместе с тем с увеличением m возрастает угол j _m между нормалью к поверхно­сти и направлением в точку Р, что приводит к уменьшению интен­сивности излучения m -й зоны в данном направлении, т.е. к уменьше­нию амплитуды А_m по сравнению с амплитудами предыдущих зон. Ам­плитуда А_k уменьшается также вследствие увеличения расстояния от зоны до точки Р с ростом j. В итоге

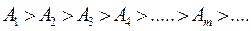
Оценка общего числа зон Френеля

.

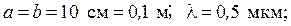
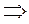
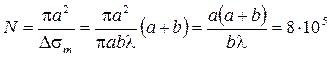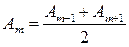
, (6)

т.е. колебания, вызываемые в точке Р полностью открытой сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только полови­на центральной зоны Френеля. Следовательно, свет от источника S ₀в точку Р распространяется в пределах очень узкого прямого канала, т.е. прямолинейно.

Оценка радиуса луча света

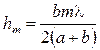
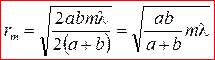; ; (7)

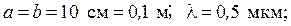
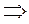
Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастает. Например, если открыты 1, 3 и 5 зоны, то

Такие пластинки, обладающие свойством подобно собирающей линзе фокусировать свет, называются зонными пластинками.

Дата добавления: 2014-01-20