Теория Аббе разрешающей способности микроскопа

Определение разрешающей способности по Аббе основано дифракционной структуре изображения в микроскопе. Это справедливо по следующим причинам – как правило, объективы микроскопов корректируются до уровня, когда аберрациями можно пренебречь. Во-вторых, изучаемые с помощью микроскопов объекты сравнимы с длиной волны, и волновыми свойствами света пренебречь нельзя и, наконец, освещение объектов можно считать с достаточной степенью когерентным, в силу теоремы Цернике[4]. Аббе было предложено в качестве тестовых объектов для микроскопов использовать периодические структуры. Это оправдано тем, что с точки зрения Фурье-анализа любую функцию, стремящуюся к нулю в бесконечности, можно представить как сумму бесконечного числа тригонометрических функций с периодами, величины которых составляют непрерывную последовательность, т.е. в виде интеграла Фурье. Ясно, что структура с таким минимальным периодом, который будет еще отображаться микроскопом, определит минимальный размер разрешаемой детали объекта, поскольку она будет одного порядка с этим периодом. Таким образом, предложенная Аббе методика вполне адекватна. Необходимо отметить, что эта идея Аббе оказалась весьма плодотворной, и ее развитие привело к появлению таких разделов оптики как теория распознавания образов и Фурье-оптика.

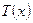На рис.15 показан объектив микроскопа 1, а предметом является синусоидальная структура 2 с периодом , функцию пропускания которой можно представить как

,

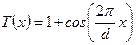(32)

где 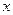- координата в плоскости изображения, "единица" добавлена как опорное (среднее) значение освещенности, так как освещенность отрицательной быть не может.

В силу предположения о когерентности освещения объекта, в задней фокальной плоскости объектива сформируется картина дифракции Фраунгофера от синусоидальной структуры, распределение освещенности в которой будет иметь вид, показанный на рисунке. График этого распределения может 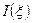быть получен в результате вычисления дифракционного интеграла в приближении Фраунгофера

,

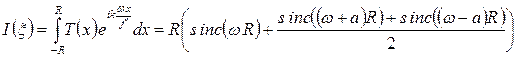(33)

где 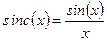- часто употребляемая сокращенная запись функции; 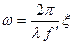- т.н. пространственная частота, величина, пропорциональная координате 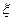в фокальной плоскости; 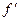- фокусное расстояние объектива;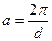;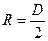. (Данный интеграл легко вычисляется, если воспользоваться формулой Эйлера 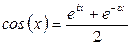). Функция исследовалась при анализе дифракции на прямоугольном отверстии, а график выражения (33) имеет вид, показанный на рис. 16. Каждый из боковых максимумов представляет собой сфокусированную плоскую дифрагированную структурой волну. В соответствии с принципом Гюйгенса-Френеля они являются источниками вторичных волн, интерференция которых сформирует изображение объекта – периодическую структуру . Покажем это. Данная ситуация аналогична той, которая возникает в опыте Юнга – здесь также происходит интерференция сферических волн, но исходящих от трех точечных источников, расположенных симметрично оптической оси. 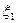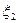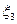Считая, что эти источники находятся в максимумах распределения рис.16, координаты которых ,иопределяются из условия, когда аргумент функции равен нулю, к примеру, из 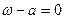следует , откуда 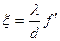. Но так как угол отклонения лучей , формирующих первый порядок дифракции на периодической структуре с периодом (у структуры с синусоидальным пропусканием имеются только два первых порядка 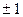) равен 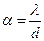, то 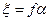, и искомые координаты определятся выражениями:

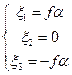
(34)

запишем уравнения этих сферических волн в плоскости изображения в приближении Френеля с амплитудами, выраженных в относительных единицах

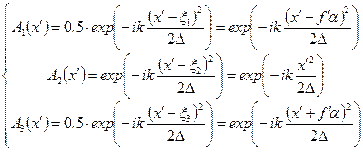
(35)

Распределение освещенности в интерференционной картине 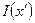будет иметь вид

.

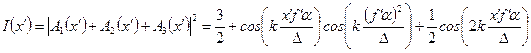(36)

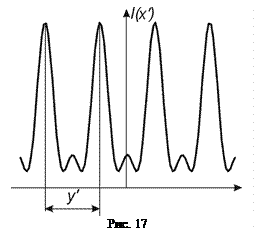График этого распределения показан на рис. 17. Первый член этого выражения представляет собой постоянную составляющую, второй член – изображение исходной периодической структуры. Действительно, период косинуса здесь определяется из соотношения

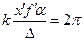. (37)

Так как 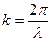, то период будет

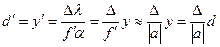, (38)

что совпадает с геометрооптическим результатом, так как увеличение будет

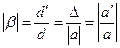. (30)

Наличие структуры с периодом 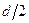(третий член) вызвано тем, что при расчете предмет (структура) находился в не в предметной плоскости, а в передней фокальной. При точном расчете эта структура исчезает.

Из изложенного следует, что изображение периодической структуры произойдет, если в фокальной плоскости образуется распределение типа приведенного на рис.17, т.е. у распределения будет два побочных максимума с координатам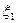и и 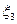. В принципе для этого достаточно, что хотя бы малая часть дифрагированных лучей прошла бы через оправу объектива микроскопа. При этом правда контраст изображения был бы невелик, так как уровень фона, который создается распределением с вершиной , был бы очень большим. Аббе предложил, что изображение удовлетворительного качества возникнет, если центральный дифрагированный луч пройдет через оправу объектива.

Из рис. 15 видно, что это наступит если . Так как предмет в микроскопе расположен вблизи фокальной плоскости объектива, то можно считать, что 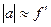. Учитывая, что 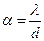получим величину минимально разрешимого объекта в микроскопе

,

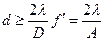(40)

где 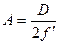- т.н. числовая апертура. Если среда между объективом и предметом имеет показатель преломления 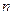, т.н. иммерсия. При этом разрешение микроскопа повышается т.к. выражение (40) примет вид (мокрый объектив)

.

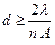(41)

Полученное соотношение носит название критерий Аббе разрешающей способности микроскопа.

Отметим аналогию критериев Релея и Аббе. В случае освещения объекта в микроскопе параллельным пучком, в объектив попадает наклонный параллельный дифрагированный пучок, который можно считать как бы исходящего из точечного источника в бесконечности. Но именно такие пучки попадают в объектив телескопа и определение разрешающей способности этих двух систем оказываются полностью эквивалентны. Наличие в критерии Релея множителя 1,22 объясняется тем, что там изначально рассматривалась дифракция на круглой апертуре. В случае же микроскопа считалось, что дифракция происходит на щели, а точнее, в двумерном случае – на квадратном отверстии – что, конечно, неверно. Этот множитель появился как отношение первого корня функции Бесселя 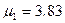(для круглого отверстия) и синуса (для квадратного отверстия) 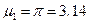(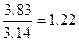). Но тем не менее эта неточность не существенна, поскольку оба критерия носят оценочный, относительный характер. Кстати, в некоторых публикациях формулу критерия Аббе записывают с таким множителем.

[1] Переменная отсутствует, поскольку предполагается, что она выражена через и в силу соотношения

[2] Это справедливо лишь для участков интерференции вблизи оси, когда для сферической волны справедливо приближение Френеля.

[3] Для распределения Эри среднеквадратическая оценка не приемлема, так как интеграл, выражающий второй момент распределения, не является сходящимся.

[4] Частный случай этой теоремы рассматривался ранее в разделе интерференция, условия когерентности, опыт Юнга.

Дата добавления: 2014-01-20