
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения переходных процессов в синхронной машине
|
|
|
|
Переходный процесс в синхронной машине может быть описан системой дифференциальных уравнений. При выводе этих уравнений приходиться вводить ряд допущений в отношении сложно учитываемых факторов:
- отсутствие потерь в магнитной системе;
- магнитная система ненасыщенна, в силу этого индуктивности машины не зависят от токов;
- в воздушном зазоре действуют только первые гармоники намагничивающей силы и индукции, при этом ЭДС статора являются синусоидами основной частоты;
- конструктивная симметрия статорных обмоток и ротора относительно своих продольной и поперечной осей.
На рис. 4.10 представлена принципиальная схема синхронной явнополюсной машины без демпферных обмоток, где стрелками указаны принятые положительные направления токов и напряжений, а также координатных осей статора (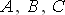 ) и ротора (
) и ротора (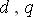 ).
).
 Рис. 4.10.
Рис. 4.10.
Рассматриваемая машина содержит четыре магнитосвязанных контура. Запишем дифференциальные уравнения равновесия ЭДС и падений напряжений. Уравнения статорных контуров записываются в неподвижных координатах фаз 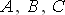 а обмотки возбуждения – в подвижных координатах ротора
а обмотки возбуждения – в подвижных координатах ротора 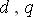 :
:

| (4.17) |

| (4.18) |
где  – мгновенные значения фазных напряжений;
– мгновенные значения фазных напряжений;
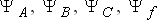 – результирующие потокосцепления обмоток статора и обмотки возбуждения;
– результирующие потокосцепления обмоток статора и обмотки возбуждения;
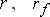 – активные сопротивления обмоток статора и цепи возбуждения.
– активные сопротивления обмоток статора и цепи возбуждения.
Знак «-» перед производной 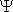 поставлен в соответствии с правилом Ленца.
поставлен в соответствии с правилом Ленца.
Раскроем выражения для потокосцеплений, которые при принятых допущениях представляют собой линейные зависимости от тока рассматриваемого контура и токов магнитосвязанных с ним контуров. Коэффициентами пропорциональности при этом является собственная индуктивность 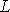 рассматриваемого контура и его взаимоиндуктивности
рассматриваемого контура и его взаимоиндуктивности  с другими контурами. Введя у
с другими контурами. Введя у 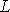 и
и  соответствующие индексы, можно записать:
соответствующие индексы, можно записать:

| (4.19) |
Здесь  и т.д.
и т.д.
Системы (4.17), (4.18) состоят из линейных дифференциальных уравнений с переменными коэффициентами. За исключением индук- тивности  , которая является постоянной величиной, все остальные
, которая является постоянной величиной, все остальные 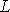 и
и  являются переменными. Они зависят от положения ротора относительно обмоток статора, что создает принципиальную сложность в решении исходной дифференциальной системы уравнений. Выясним закономерности изменения индуктивностей синхронной машины, считая, что положение магнитной оси фазы
являются переменными. Они зависят от положения ротора относительно обмоток статора, что создает принципиальную сложность в решении исходной дифференциальной системы уравнений. Выясним закономерности изменения индуктивностей синхронной машины, считая, что положение магнитной оси фазы 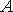 и продольной оси ротора
и продольной оси ротора 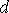 характеризуются углом
характеризуются углом 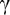 (рис. 4.12).
(рис. 4.12).
Взаимоиндуктивности 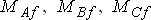 зависят от положения ротора (
зависят от положения ротора (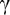 ). Принятое допущение о синусоидальности наводимых в статоре ЭДС указывает на закономерности их изменения. Взаимная индуктивность
). Принятое допущение о синусоидальности наводимых в статоре ЭДС указывает на закономерности их изменения. Взаимная индуктивность  получается максимальной (
получается максимальной (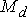 ) при
) при 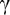 =0 и выражается синусоидальной функцией с периодом
=0 и выражается синусоидальной функцией с периодом 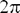
 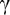
| (4.20) |
для фаз B и C используются аргументы (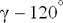 ) и (
) и ( ).
).
Собственная индуктивность фаз 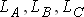 зависит от положения ротора (). Она получается наибольшей для любой из фаз, когда продольная ось ротора совпадает с магнитной осью соответствующей фазы статора, и наименьшей, когда эти оси перпендикулярны (
зависит от положения ротора (). Она получается наибольшей для любой из фаз, когда продольная ось ротора совпадает с магнитной осью соответствующей фазы статора, и наименьшей, когда эти оси перпендикулярны (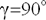 ). Следовательно, собственная индуктивность изменяется гармонически с периодом, т.е. с двойной частотой и не зависит от направления вращения ротора. В частности для фазы имеем:
). Следовательно, собственная индуктивность изменяется гармонически с периодом, т.е. с двойной частотой и не зависит от направления вращения ротора. В частности для фазы имеем:
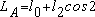 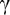
| (4.21) |
Фазам (2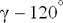 ) и (2
) и (2 ) соответствуют аргументы () и ().
) соответствуют аргументы () и ().
Взаимная индуктивность фаз статора  является величиной отрицательной и достигает наименьшего абсолютного значения когда ось
является величиной отрицательной и достигает наименьшего абсолютного значения когда ось 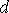 совпадает с биссектрисой угла, образованного осями фаз статора. Она изменяется гармонически с периодом и между фазами
совпадает с биссектрисой угла, образованного осями фаз статора. Она изменяется гармонически с периодом и между фазами 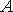 и
и 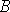 определяется выражением
определяется выражением
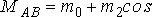 (2 (2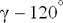 ) )
| (4.22) |
Взаимной индуктивности фаз B и C соответствует аргумент 2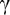 , а фаз A и C – аргумент (2
, а фаз A и C – аргумент (2 ).
).
Коэффициенты в (4.21), (4.22) можно выразить через индуктивности, которыми обычно характеризуется синхронная машина [11]. В относительных единицах эта взаимосвязь имеет вид:
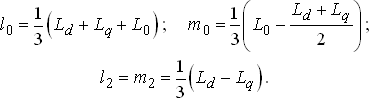
Исходная система дифференциальных уравнений (4.17), (4.18) с учетом найденных закономерностей для собственных и взаимных индуктивностей имеет переменные во времени коэффициенты. По этой причине решение дифференциальных уравнений не может быть найдено в элементарных функциях.
Решение этой проблемы предложили Р.Х. Парк и А.А. Горев. Основная идея их предложения заключается в замене трехфазной машины эквивалентной двухфазной, что соответствует переходу от трехосевой (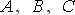 ) к двухосевой (
) к двухосевой (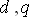 ) системе координат. Вторым, наиболее важным моментом является то, что двухосевая система координат расположена не на статоре, а предполагается жестко связанной с ротором. Это равносильно замене трех неподвижных обмоток статора двумя обмотками, вращающихся вместе с ротором. Так как фазные обмотки, расположенные в осях
) системе координат. Вторым, наиболее важным моментом является то, что двухосевая система координат расположена не на статоре, а предполагается жестко связанной с ротором. Это равносильно замене трех неподвижных обмоток статора двумя обмотками, вращающихся вместе с ротором. Так как фазные обмотки, расположенные в осях 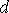 и
и 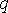 , неподвижны относительно роторной обмотоки, все индуктивности такой машины постоянны. Это позволяет заменить исходную систему дифференциальных уравнений новой с постоянными коэффициентами, решение которой не представляет принципиальных сложностей. Указанное преобразование наиболее просто осуществляется с использованием обобщенного вектора трехфазной системы.
, неподвижны относительно роторной обмотоки, все индуктивности такой машины постоянны. Это позволяет заменить исходную систему дифференциальных уравнений новой с постоянными коэффициентами, решение которой не представляет принципиальных сложностей. Указанное преобразование наиболее просто осуществляется с использованием обобщенного вектора трехфазной системы.
Мгновенное значение любой синусоидальной величины можно представить в виде проекции вращающегося вектора на неподвижную ось времени. Если речь идет о симметричной трехфазной системе, то в этом случае проекции симметричной звезды трех векторов на единую ось времени дают мгновенные значения фазных величин (рис. 4.11, а). Однако, те же мгновенные значения фазных величин можно получить, проецируя единый вектор на три оси времени, каждая из которых совпадает с магнитной осью соответствующей фазы (рис. 4.11, б). Такой вектор называется обобщенным вектором трехфазной системы. При его вращении в ту же сторону, что и системы трех векторов, чередование осей времени фаз нужно изменить на противоположное. При симметричном установившемся режиме обобщенный вектор вращается с неизменной синхронной скоростью и постоянен по абсолютной величине. Обобщенным вектором можно характеризовать любые фазные переменные ( ).
).
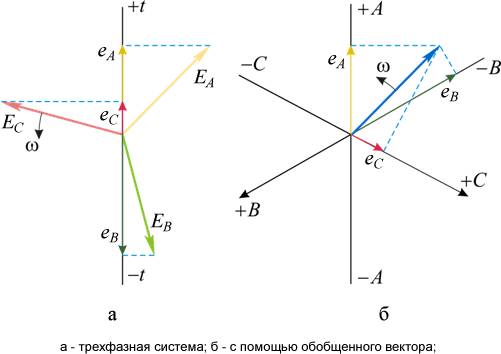
Рис. 4.11. К определению мгновенных значений векторов
Произведем замену переменных, для чего выразим величины фаз статора ( ) через соответствующие величины в координатах
) через соответствующие величины в координатах 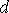 ,
, 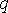 , вращающихся вместе с ротором. Для этого воспользуемся схемой (рис. 4.12), где через
, вращающихся вместе с ротором. Для этого воспользуемся схемой (рис. 4.12), где через 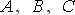 обозначены неподвижные координаты фаз статора (фазные оси времени), через
обозначены неподвижные координаты фаз статора (фазные оси времени), через 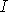 – обобщенный вектор тока.
– обобщенный вектор тока.
Проекция вектора 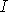 на ось A дает
на ось A дает 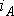 , а на оси
, а на оси 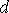 и
и 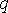 соответственно
соответственно 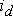 и
и 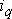 . Проецируя токи
. Проецируя токи 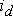 и
и 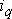 на ось A, находим интересуемую связь между фазным током и токами в новой системе координат
на ось A, находим интересуемую связь между фазным током и токами в новой системе координат

| (4.23) |
что отражает сущность замены переменных.
Фазе B соответствует аргумент (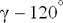 ) и C – аргумент (
) и C – аргумент ( ).
).
Преобразования были сделаны в предположении, что трехфазная система являлась уравновешенной, т.е.

| (4.24) |

Рис. 4.12. Связь параметров (токов) неподвижной системы координат 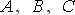 с подвижной
с подвижной 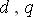
Если нейтраль заземлена и указанные условия не выполняются, то следует ввести дополнительное соотношение, известное из теории симметричных составляющих для токов нулевой последовательности:
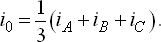
| (4.25) |
Поскольку нулевая составляющая 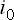 во всех фазах одинакова, она не влияет ни на обобщенный вектор, ни на его проекции на оси
во всех фазах одинакова, она не влияет ни на обобщенный вектор, ни на его проекции на оси 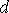 и
и 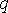 . Поэтому в общем случае при переходе к фазным переменным необходимо в уравнении (4.23) учесть нулевую составляющую
. Поэтому в общем случае при переходе к фазным переменным необходимо в уравнении (4.23) учесть нулевую составляющую
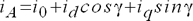
| (4.26) |
Обратимся к преобразованию дифференциальных уравнений (4.17) путем замены фазных переменных их составляющими в координатах 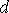 ,
, 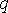 , 0.
, 0.
В соответствии со структурой выражения (4.26) представим напряжение и потокосцепление фазы 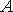 через новые переменные:
через новые переменные:
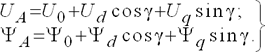
| (4.27) |
Подставляя 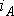 согласно (4.26), а
согласно (4.26), а  из выражений (2.27) в первое уравнение (4.17) и имея в виду при дифференцировании, что
из выражений (2.27) в первое уравнение (4.17) и имея в виду при дифференцировании, что 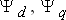 и
и 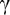 являются функциями времени
являются функциями времени 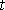 , получим:
, получим:

После перегруппировки слагаемых это выражение можно представить в виде:

| (4.28) |
Уравнение (2.28) должно быть удовлетворено при любом значении 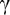 , что возможно только при условии, что каждое из выражений, заключенных в скобках, тождественно равно нулю. При этом соотношение (4.28) распадается на три уравнения:
, что возможно только при условии, что каждое из выражений, заключенных в скобках, тождественно равно нулю. При этом соотношение (4.28) распадается на три уравнения:
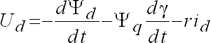
| (4.29) |

| (4.30) |

| (4.31) |
Результат преобразования не изменится, если вместо фазы A рассматривать иную фазу.
Уравнение для обмотки возбуждения сохраняется неизменным (4.18), поэтому оно повторно не приведено.
В уравнениях (4.29) – (4.31) для системы относительных единиц потокосцепления определяются выражениями:

| (4.32) |
где 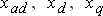 – являются известными реактивностями, которыми характеризуется синхронная машина в продольной и поперечной осях для действующих значений токов;
– являются известными реактивностями, которыми характеризуется синхронная машина в продольной и поперечной осях для действующих значений токов;
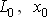 – индуктивность и индуктивное сопротивление нулевой последовательности.
– индуктивность и индуктивное сопротивление нулевой последовательности.
Таким образом, переход к новым переменным в координатах 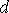 ,
, 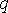 , 0 позволил получить систему дифференциальных уравнений с постоянными коэффициентами.
, 0 позволил получить систему дифференциальных уравнений с постоянными коэффициентами.
Уравнения (2.29) – (2.31) называют уравнениями Парка-Горева.
Наглядную физическую интерпретацию составляющим уравнений Парка-Горева можно дать, пользуясь понятием обобщенного вектора потокосцепления. В переходном режиме обобщенный вектор потокосцепления, вращаясь с несинхронной скоростью изменяется по величине. Поэтому слагаемые 
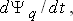
 – отражают трансформаторные ЭДС, обусловленные изменением потокосцеплений по величине. Слагаемые
– отражают трансформаторные ЭДС, обусловленные изменением потокосцеплений по величине. Слагаемые  ,
, 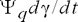 – обусловлены перемещением (вращением) потокосцеплений; их называют ЭДС вращения.
– обусловлены перемещением (вращением) потокосцеплений; их называют ЭДС вращения.

|
Следовательно, 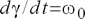 и в относительных единицах при
и в относительных единицах при  имеем
имеем  .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1229; Нарушение авторских прав?; Мы поможем в написании вашей работы!