Вязкость

Вязкость (внутреннее трение) (см. лекцию №5 «Элементы механики жидкостей и газов») возникает между слоями газа или жидкости, движущимися с разными скоростями. Если скорость направленного движения слоёв газа изменяется вдоль оси OZ (рис.7.6), то по закону Ньютона, импульс, перенесённый через малую площадку 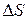за время 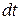, пропорционален градиенту скорости направленного движения слоёв :

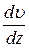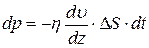, (7.13)

где 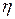– динамическая вязкость. Быстрый слой при этом тормозится, медленный – ускоряется в результате действия силы вязкого трения:

.

Из (7.13) физический смысл динамической вязкости: коэффициент вязкости 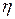численно равен импульсу, перенесённому из слоя в слой через единичную площадку за единицу времени при единичном градиенте скорости направленного движения слоёв. Размерность коэффициента вязкости:

.

Плотность потока импульса (импульс, перенесённый за единицу времени через единичную площадку) равна

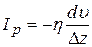. (7.14)

5. Теплопроводность.

Пусть вдоль оси OZ изменяется температура (рис.7.7). Опыт показывает, что количество теплоты, перенесённой через малую площадку 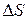за время 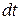в результате теплопроводности, пропорционально градиенту температуры :

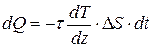. (7.15)

Здесь – коэффициент теплопроводности. Его физический смысл: численно равен количеству теплоты, перенесённой через единичную площадку за единицу времени при единичном градиенте температуры. Размерность

.

Знак «минус» в уравнении теплопроводности (7.15) означает, теплота переносится из области с большей температурой в область с меньшей температурой. Введём плотность потока тепловой энергии: – количество теплоты, перенесённой за единицу времени через единичную площадку, перпендикулярную направлению переноса. Так же как для двух предыдущих явлений переноса, для теплопроводности можно записать уравнение переноса через плотность потока тепловой энергии:

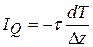. (7.16)

Уравнение теплопроводности (7.15), (7.16) – это закон Фурье.

6. Явления переноса в твёрдых и жидких телах также имеют место. Однако диффузия в жидкостях протекает медленнее, чем в газах, а для некоторых твёрдых тел при комнатной температуре практически не заметна. Это объясняется меньшей подвижностью частиц в конденсированной фазе, более плотной упаковкой частиц, а также тем, что частицы взаимодействуют друг с другом. Молекула жидкости некоторое время колеблется около своего положения равновесия, и изменяет его, перескакивая в соседнее положение, если затратит энергию, равную энергии активации. С ростом температуры число молекул жидкости, имеющих энергию, достаточную для преодоления этого потенциального барьера, возрастает, и подвижность молекул растёт. Это приводит к увеличению коэффициента диффузии жидкости. Коэффициент вязкости жидкости, напротив, с ростом температуры уменьшается, так как молекулы легче меняют своё положение и, например, при движении тела в жидкости легче «пропускают» его, перестраиваясь в другое положение. Сами же коэффициенты вязкости для жидкостей на несколько порядков больше, чем для газов.

Теплопроводность жидких и твёрдых тел больше, чем газов. Это объясняется взаимодействием частиц, в результате которого тепловая энергия передаётся быстрее. У металлов теплопроводность большая за счёт очень подвижных электронов.

Пористые твёрдые тела являются хорошими теплоизоляторами – за счёт пор, заполненных воздухом.

7. Коэффициенты переноса в газах.

Молекулярно-кинетическая теория идеального газа позволяет получить уравнения переноса теоретическим путём и дать выражение для коэффициентов переноса. Молекулы газа, двигаясь хаотически, переходят в другие части системы и переносят массу, импульс, связанный с направленным движением слоёв газа, либо тепловую энергию.

а) Коэффициент диффузии

Пусть концентрация уменьшается с координатой Z по какому-либо закону (рис.7.5). Пусть слева от площадки концентрация больше, чем справа: .

Выберем малую площадку 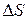, перпендикулярную оси OZ. Будем считать, что все молекулы могут двигаться только параллельно координатным осям и имеют одинаковые скорости теплового движения, равные средней арифметической . Площадку могут пересечь молекулы, которые летели по направлению к ней, а это часть всех молекул: ещё летит от площадки тоже параллельно оси OZ, и ещё по движутся параллельно двум другим осям. За время 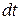до площадки дойдут те молекулы, которые были от площадки на расстоянии не больше, чем , то есть находились в объёме . Концентрация молекул слева от площадки , поэтому число молекул, пересекающих площадку слева направо за время 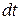, равно:

. (7.17)

Аналогично, число молекул, пересекающих площадку справа налево тот же промежуток времени, равно:

. (7.18)

Результирующий перенос будет в положительном направлении оси OZ:

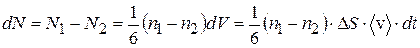. (7.19)

Возникает вопрос: где именно, как далеко от площадки, нужно взять концентрации и ? Последний раз перед пересечением площадки молекулы сталкиваются с другими молекулами и изменяют направление движения на расстоянии от площадки, равном длине свободного пробега; следовательно, они перенесут через неё информацию о концентрации, сложившуюся на расстоянии 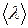от площадки. Тогда, если функция достаточно гладкая, можно записать производную её по координате как отношение конечных приращений (см. рис.7.5):

. (7.20)

В (7.20) учтено, что производная 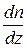убывающей функции отрицательна, а . Далее, из (7.19) и (7.20) получим:

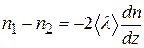
. (7.21)

Сравнив (7.21) с (7.11), получим, что коэффициент диффузии равен

. (7.22)

б) Коэффициент вязкости

При выводе формулы для коэффициента вязкости рассуждения аналогичны. Пусть скорость направленного движения слоёв газа убывает с координатой Z (рис.7.6). Концентрации молекул слева и справа одинаковы, и за время 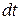площадку пересечёт одинаковое число молекул, равное

. (7.23)

Импульс молекул, находящихся слева от площадки, связанный с направленным движением слоёв газа, равен . Эти молекулы перенесут слева направо импульс суммарный :

.

Аналогично, в обратном направлении будет перенесён импульс

.

Результирующий перенос:

. (7.24)

Молекулы, переходя из более быстрого слоя, движущегося со скоростью 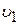, в более медленный слой, движущийся со скоростью , переносят свой импульс, связанный с направленным движением слоёв, и медленный слой в целом ускоряется. Наоборот, более медленные молекулы переходят в быстрый слой и в целом его притормаживают. Это и проявляется как вязкость: скорости направленного движения слоёв выравниваются.

Аналогично (7.20) выразим производную 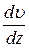(градиент скорости направленного движения):

. (7.25)

Молекулы, переходя через площадку, переносят через неё импульсы, связанные с теми скоростями направленного движения, которые сложились на расстоянии 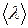от площадки. Из (7.24) и (7.25):

,

. (7.26)

Сравнив (7.26) и (7.13), получим коэффициент динамической вязкости:

, (7.27)

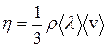, (7.28)

так как плотность .

Коэффициент вязкости газа с ростом температуры при постоянном давлении растёт: и за счёт увеличения скорости хаотического движения:

,

и за счёт увеличения длины свободного пробега (7.8б): .

в) Коэффициент теплопроводности

Пусть вдоль оси OZ изменяется температура (рис.7.7).

В результате теплового движения молекулы переносят через площадку свои средние тепловые энергии, которые сложились на расстоянии 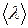от площадки в точках с координатами и . Средняя энергия молекулы равна ; здесь – число степеней свободы молекулы (см. предыдущую лекцию). Тогда тепловая энергия, перенесённая слева направо, равна

,

а в обратную сторону

.

Результирующий перенос с учётом (7.23):

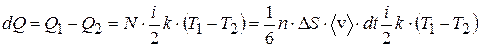. (7.28)

Градиент температуры равен:

,

тогда

. (7.29)

Сравнивая (7.29) и (7.15), получим коэффициент теплопроводности:

. (7.30)

Преобразуем его, учтя, что

,

,

.

Тогда

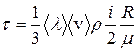
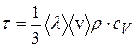, (7.31)

где – молярная теплоёмкость газа при постоянном объёме; – его удельная теплоёмкость (подробнее теплоёмкостях в лекции «Термодинамика»).

Коэффициент теплопроводности при постоянной температуре не зависит от давления: из (7.8) и (7.31) следует:

,

то есть не меняется, потому что плотность и концентрация изменяются синхронно; уменьшение плотности компенсируется увеличением 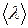. Но если газ достиг состояния вакуума, то в качестве длины свободного пробега нужно брать расстояние между стенками сосуда, и . Уменьшение плотности ничем не компенсируется, и теплопроводность разреженного газа уменьшается. Это используется практически в обычных бытовых термосах, имеющих двойные стенки, между которыми вакуум – разреженный воздух. За счёт вакуума достигнута малая теплопроводность стенок термоса.

Дата добавления: 2014-01-20