Структура нейронов. Типы нейронов

Теоретические предпосылки эффективности НС

В 1943 Маккаллок и Питтс предложили модель “порогового логического нейрона” (сигнал на выходе нейрона появляется только после превышения суммы взвешенных входных сигналов) и показали, что любая функция, которая может быть вычислена на ЭВМ, может быть вычислена и сетью нейронов.

Ряд важных теоретических результатов был получен в результате многолетней полемики между А.Н. Колмогоровым и В.И. Арнольдом (теорема Колмогорова-Арнольда):

•Теорема о возможности представления непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных (1956 г.).

•Теорема о представлении любой непрерывной функции трех переменных в виде суммы функций не более двух переменных (1957 г.).

•Теорема о представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одной переменной и сложения (1957 г.).

Последняя теорема была переложена Хехт-Нильсеном в 1987 г. для нейронных сетей. Уточненная формулировка теоремы Хехт-Нильсена заложена в теорему о полноте: Любая непрерывная функция на замкнутом ограниченном множестве может быть равномерно приближена функциями, вычисляемыми нейронными сетями, если функция активации нейрона дважды непрерывно дифференцируема и непрерывна. Указанными свойствами обладает сигмоидальная функция активации.

Адаптивный сумматор

Адаптивный сумматор реализует функцию скалярного произведения вектора входов нейрона на вектор весов. Адаптивным он называется, поскольку вектор весов W является настраиваемым.

Нелинейный преобразователь

Нелинейный преобразователь реализует функцию возбуждения нейрона. Известны три основных типа функции возбуждения:

а) пороговая;

б) линейная;

в) сигмоидальная (наиболее приближенная к реальному нейрону).

Точка ветвления

Предназначена для рассылки одного сигнала по нескольким адресам.

Синапс

Отдельно от сумматоров не встречается, выделяется для удобства рассуждений. Представляет собой линейную связь с коэффициентом усиления.

Стандартный формальный нейрон состоит из сумматора, нелинейного преобразователя и точки ветвления:

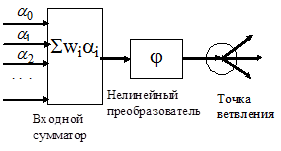
Наиболее распространены два типа нейронов: нейрон Хебба (он более распространен, приведен на рис.) и нейрон Олбуса. НС, построенные на нейронах Хебба, называют сетями с синаптической пластичностью, построенные на нейронах Олбуса - сетями с нейронной пластичностью.

У нейрона Олбуса сумматор производит только суммирование, а умножение на коэффициент осуществляется после нелинейного преобразователя, или после точки ветвления (в этом случае умножение производится также на вектор коэффициентов для каждого выхода).

Нелинейный преобразователь – некоторая функция, называемая активационной функцией.

Дата добавления: 2014-01-20