
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегрирование по частям
|
|
|
|
При этом способе используют формулу интегрирования по частям
∫udv=uv-∫vdu (*)
К числу интегралов, вычисляемых по частям, относятся, например, интегралы вида ∫P(x)·f(x)dx, где P(x)- многочлен (в частности, степенная функция), а f(x)- одна из следующих функций: ex, sin ax, cos ax, ln x, arcsin x, arccos x, arctg x, arcctg x. При этом для интегралов вида ∫P(x)·eaxdx, ∫P(x) sin axdx, ∫P(x) cos axdx, в качестве “u” принимают многочлен P(x), а для интегралов вида ∫P(x) arcsin xdx, ∫P(x) arccos xdx, ∫ P(x) arctg xdx, ∫ P(x) arcctg xdx, ∫P(x) ln xdx в качестве “u” принимается ln x, arcsin x, arccos x, arctg x, arcctg x.
Пример. Решить методом интегрирования по частям ∫ x ln xdx.
Решение. Согласно данным выше рекомендациям, заменим lnx=u, а оставшееся выражение xdx=dv. Найдем du=d(lnx)=dx/x и функцию v из равенства dv=xdx. Тогда ∫dv=∫xdx, откуда v=x2/2 (полагаем С=0). Теперь, зная u=lnx, v=x2/2 и du=dx/x, применим формулу интегрирования по частям ∫udv = uv-∫vdu. В нашем примере имеем:
∫lnx·xdx=  или ∫xlnxdx=
или ∫xlnxdx=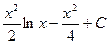 .
.
Примечание: В некоторых случаях для приведения интеграла к табличному виду формулу интегрирования по частям применяют последовательно несколько раз.
Интегрирование рациональных дробей.
Рациональной функцией называется функция вида 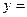
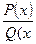 , где
, где  и
и  - многочлены.
- многочлены.
Рациональная дробь 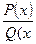 называется правильной, если степень многочлена
называется правильной, если степень многочлена  меньше степени многочлена
меньше степени многочлена  . Если рациональная дробь
. Если рациональная дробь  не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде
не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде  , где
, где 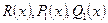 - некоторые многочлены, а
- некоторые многочлены, а  - правильная рациональная дробь.
- правильная рациональная дробь.
Теорема. Пусть 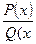 - правильная рациональная дробь,
- правильная рациональная дробь,  и
и  - многочлены с действительными коэффициентами. Если многочлен
- многочлены с действительными коэффициентами. Если многочлен  представляет собой
представляет собой 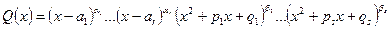 , где
, где 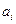 - попарно различные действительные корни многочлена
- попарно различные действительные корни многочлена  кратности
кратности 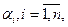 а
а 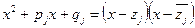 , где
, где 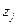 и
и 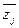 - попарно различные при разных
- попарно различные при разных 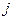 комплексно-сопряженные корни многочлена
комплексно-сопряженные корни многочлена  кратности
кратности 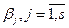 , то существуют действительные числа
, то существуют действительные числа 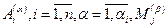 и
и  , такие, что
, такие, что 
При выполнении разложения вида (*) для конкретно заданной дроби оказывается удобным так называемый метод неопределенных коэффициентов. Он состоит в следующем. Для данной дроби 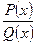 пишется разложение (*), в котором коэффициенты
пишется разложение (*), в котором коэффициенты 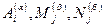 считаются неизвестными
считаются неизвестными  . После этого обе части равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты. При этом если степень многочлена
. После этого обе части равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты. При этом если степень многочлена  равна
равна  , то получаем систему
, то получаем систему  уравнений с
уравнений с  неизвестными. Решая ее, находим неизвестные коэффициенты.
неизвестными. Решая ее, находим неизвестные коэффициенты.
Теорема. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно, он является алгебраической суммой суперпозиций рациональных дробей, арктангенсов и натуральных логарифмов.
Интегрирование тригонометрических и иррациональных выражений.
Интегрирование некоторых иррациональностей.
Интегралы вида 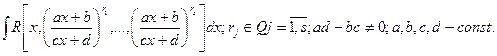
Пусть 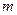 - общий знаменатель чисел
- общий знаменатель чисел 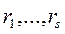 .Тогда замена
.Тогда замена 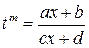 приводит искомый интеграл к интегралу от рациональной функции.
приводит искомый интеграл к интегралу от рациональной функции.
Интегралы вида  приводят к интегралам предыдущего вида путем элементарного преобразования:
приводят к интегралам предыдущего вида путем элементарного преобразования: 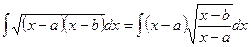 .
.
Интегралы от дифференциального бинома. Подстановки Чебышева.
Выражение 
 называется дифференциальным биномом. Здесь
называется дифференциальным биномом. Здесь 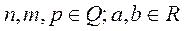 . Замена
. Замена 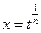 приводит
приводит  к интегралу типа
к интегралу типа  .
.
П.Л. Чебышев показал, что данный интеграл выражается через элементарные функции только в трех случаях:
1.  замена:
замена: 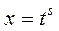 , где
, где 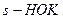 знаменателей дробей
знаменателей дробей 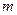 и
и  .
.
2. 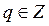 замена:
замена: 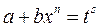 , где
, где  знаменатель дроби
знаменатель дроби  .
.
3.  замена:
замена:  , где
, где  знаменатель дроби
знаменатель дроби  .
.
Тригонометрические подстановки.
Интегралы вида  приводятся к интегралам от рациональной относительно
приводятся к интегралам от рациональной относительно 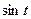 и
и  функции с помощью надлежащей тригонометрической подстановки: для первого интеграла
функции с помощью надлежащей тригонометрической подстановки: для первого интеграла  (или
(или  ), для второго
), для второго  (или
(или 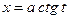 ) и для третьего
) и для третьего 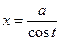 (или
(или 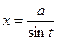 ).
).
Универсальная тригонометрическая подстановка.
Замена всех тригонометрических функций тангенсом половинного угла

приводит интегралы вида  к интегралам от рациональных функций.
к интегралам от рациональных функций.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1224; Нарушение авторских прав?; Мы поможем в написании вашей работы!