
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Гаусса. Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля
|
|
|
|
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая малая площадка Δ S. Произведение модуля вектора 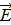 на площадь Δ S и на косинус угла α между
на площадь Δ S и на косинус угла α между
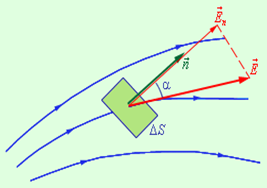 Рисунок 1.7. К определению элементарного потока ΔΦ
Рисунок 1.7. К определению элементарного потока ΔΦ
| вектором 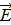 и нормалью и нормалью 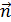 к площадке называется элементарным потоком вектора к площадке называется элементарным потоком вектора
ΔΦ = E Δ S cos α = En Δ S, (1.8) где En – модуль нормальной составляющей поля
|
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
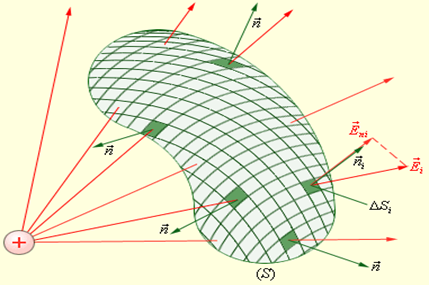 Рисунок 1.8 Вычисление потока Ф через
произвольную замкнутую поверхность S
Рисунок 1.8 Вычисление потока Ф через
произвольную замкнутую поверхность S
| Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля 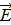 через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0. через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
 1.10) 1.10)
|
Для доказательства рассмотрим сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю

где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4π R 2. Следовательно, Ф = q / .
.
Применив теорему Гаусса, можно вычислить поля:
1) Тонкостенного полого однородно заряженного длинного цилиндра радиуса R
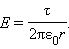 , (1.11)
, (1.11)
где r ≥ R, τ – заряд единицы длины цилиндра. Если r 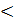 R, Е= 0. Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
R, Е= 0. Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
2) Равномерно заряженной плоскости:
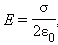 (1.12)
(1.12)
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 389; Нарушение авторских прав?; Мы поможем в написании вашей работы!
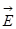 сквозь неё:
сквозь неё: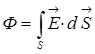 . (1.9)
. (1.9)