Распределение Пуассона. Дискретная случайная величина называется распределенной по закону Пуассона, если она принимает счетное множество значений 0

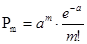Дискретная случайная величина называется распределенной по закону Пуассона, если она принимает счетное множество значений 0, 1, 2, …с вероятностями

Это распределение содержит один параметр а.

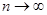Если и при этом, но произведение np остается постоянным, а именно np=a, то биномиальное распределение в пределе дает распределение Пуассона. Поэтому закон Пуассона в литературе часто называется «законом редких явлений».

Распределение Пуассона применяется, когда n порядка нескольких сотен и больше, а 1≤ np ≤ 10.

Числовые характеристики:

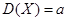• Математическое ожидание

• Дисперсия

• Среднее квадратическое отклонение

Доказано, что распределение Пуассона имеет случайная величина Х, являющаяся числом появлений событий в простейшем потоке за промежуток времени t. При этом параметр распределения Пуассона.

Дискретные случайные величины – число вызовов на станцию скорой помощи, число автомашин, проходящих ночью мимо поста ГАИ, число авиалайнеров, прибывающих в аэропорт, число требований на выплату страховых сумм за некоторый период времени t имеют распределение Пуассона с параметром.

Пример 2. Мимо поста ГАИ ночью проходят автомашины с интенсивностью 5 автомашин в час. Найти вероятность того, что за 3 часа:
1) пройдут 4 автомашины; 2) не менее двух машин; 3) хотя бы одна машина.

Решение: Находим параметр авт.

1) Вероятность того, что за 3 часа пройдут 4 автомашины, равна

2) Пусть событие

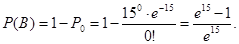
3) Пусть событие

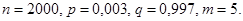Пример 3. Завод отправил на базу 2000 доброкачественных изделий. Вероятность того, что изделие в пути выйдет из строя, равна 0,003. Найти вероятность того, что на базу прибудут 5 бракованных изделий.

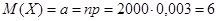Решение. Имеем:

Определяем

Дата добавления: 2014-01-20