Исключение квантора существования

Если А не содержит х, то очевидно: xA = A и xA = A. "Очевидно" - потому что кванторы здесь ничего не определяют и не дают. Это элементарный пример исключения кванторов.

Рассмотрим теперь формулу xP (x) (существует хотя бы один х, при котором Р (x) = И). Пусть этот х будет равен с, тогда указанная формула запишется просто P (с). Константа с любая, однако, она не должна совпадать с другими символами, применяемыми в других формулах. Это - второй пример исключения квантора существования. Он касается случая, когда сам квантор не находится в области действия какого-либо квантора общности.

Рассмотрим теперь формулу xyP (x,y) (для всех х существует по крайней мере один y такой, что выполняется предикат P (x,y)). Ясно, что y, удовлетворяющий этому условию, как-то зависит от х. Эту зависимость можно отобразить с помощью некоторой функции, например, g(x). Эта функция теперь заменяет y, а квантор существования можно просто убрать:

xP (x,g (x)).

Функция типа g (x), отображающая каждое значение х в "тот самый y ", называется функцией Сколема или сколемовской.

Особенности:

1) если квантор стоит перед квантором общности , то он не находится в области его действия и поэтому заменяется, как в прежнем примере, некоторой константой:

xyP (x,y) = yP (a,y).

2) если квантор находится в области действия нескольких кванторов общности, то соответствующая его переменная заменяется сколемовской функцией от соответствующего числа переменных (мест):

xyr wP (x,y,r,w) = xyrP (x,y,r,g (x,y,r)) -

"собственная" переменная квантора существования w заменяется сколемовской функцией g, зависящей от всех квантифицированных переменных, в сфере действия которых она находится.

3) Следующий пример говорит сам за себя:

xyP (x,y) = P (a,b).

4) Еще один пример: x [ P (x,y) 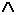y (M (y,z) R (y,z,q))] =x [(P (x,y) 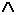(M (g (x) ,z) R (g (x) ,z,q))].
Сколемовская функция g (x) заменяет y во всех местах его вхождения в области действия квантора .

Рассмотрим и осмыслим теперь такой обобщающий пример:

5) Дано: zxuyrwsvqM (z,x,u,y,r,w,s,v,q).

После сколемизации:

xyrvM (а,x,f (x) ,y,r,g (x,y,r) ,h (x,y,r) ,v,p (x,y,r,v)).

Дата добавления: 2014-01-20