
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обобщающий пример
|
|
|
|
Приведение матрицы к КНФ
Исключение кванторов общности
Получение предваренной формы - важный этап в деле преобразования исходной формулы ИП. Дальнейшая работа будет проводиться с матрицей, все переменные которой относятся к тому или иному квантору общности. Роль цепочки кванторов (префикса) в данном случае - в простом напоминании об этом факте. К тому же порядок кванторов общности роли не играет. Если все это принять во внимание, то префикс вообще можно убрать и предположить по соглашению, что все переменные относятся к своим кванторам общности. Остается одна матрица.
Если теперь рассматривать матрицу как логическое выражение, связывающее посредством пропозициональных связок некоторое количество литералов, то процесс приведения любой матрицы к конъюнктивной нормальной форме будет мало чем отличаться от такого же процесса в рамках исчисления высказываний. Процесс этот всегда возможен, и конечный итог известен: матрица будет представлена в виде конъюнкции дизъюнктов (каузальная форма). Дизъюнкт, напомним, в исчислении предикатов называется предложением. Знаки конъюнкции можно опустить, и все множество полученных предложений представить в виде столбца, рассматривая каждое из них как некую исходную гипотезу (как это мы делали с дизъюнктами в процессе логического вывода в ИВ).
Привести заданное выражение к системе предложений.
 x {
x {  y [ P (x,y)
y [ P (x,y) 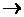
 xQ (x, h (y))]
xQ (x, h (y))] 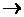
 x
x  yR (a,y,x)}.
yR (a,y,x)}.
Освобождаемся от импликаций.
 x {
x {  y [
y [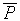 (x,y)
(x,y) 
 xQ (x,h (y))]
xQ (x,h (y))] 
 x
x  yR (a,y,x)}.
yR (a,y,x)}.
Переносим и снимаем отрицания (согласно (6.6) и др. правилам).
 x {
x {  y
y 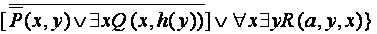
 x {
x {  y
y 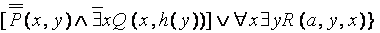 .
.
Окончательно:
 x {
x {  y
y 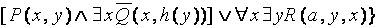 .
.
Проводим стандартизацию: каждый квантор должен иметь свою переменную. С этой целью переименуем в средней формуле (для  ) x на u, в последней формуле - x на z, y на w:
) x на u, в последней формуле - x на z, y на w:
 x {
x {  y
y  }.
}.
Исключаем кванторы существования. Заметим, что квантор  y находится в сфере действия
y находится в сфере действия  x и распространяется на квадратные скобки, а квантор
x и распространяется на квадратные скобки, а квантор  w - в сфере действия
w - в сфере действия  x и
x и  z, соответственно вводим функции Сколема.
z, соответственно вводим функции Сколема.
 x {
x {  }.
}.
Выносим кванторы общности влево, за скобки, образуем предваренную форму.
 x
x  u
u  z {
z { 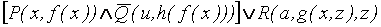 }.
}.
Опускаем кванторы общности, полученную матрицу приводим к КНФ.
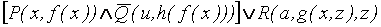 =
=
(раскрывая конъюнкцию по дизъюнкции)
= (P (x,f (x))  R (a,g (x,z) ,z))
R (a,g (x,z) ,z)) 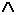 (
(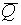 (u,h (f (x)))
(u,h (f (x)))  R (a,g (x,z) ,z))
R (a,g (x,z) ,z))
Окончательно получаем систему предложений:
1. P (x,f (x))  R (a,g (x,z) ,z)),
R (a,g (x,z) ,z)),
2. `Q (u,h (f(x)))  R (a,g (x,z) ,z)).
R (a,g (x,z) ,z)).
Хорошо, что мы научились приводить выражение в предваренной форме к системе предложений. Но для того, чтобы идти дальше и проводить с ними процесс резолюции, нам необходимо уметь находить контрарные литералы, что при участии многоместных предикатов с различными переменными становится делом весьма непростым. Пусть, например, имеются предложения:
1. Q (u)  P (A),
P (A),
2.`Q (w)  P (w),
P (w),
3.`Q (x)  `P (x)
`P (x)
4. Q (y)  `P (y).
`P (y).
Судя по предикатным символам, здесь вполне возможна резолюция. Но различные переменные не дают нам делать это непосредственно. Необходимо делать подстановки.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 389; Нарушение авторских прав?; Мы поможем в написании вашей работы!