Тема 10

Тема 9

Тема 8

Тема 7

Тема 6

Тема 5

«Движение жидкости внутри рабочего колеса центробежного насоса (треугольники скоростей на входе и выходе из рабочего колеса)»

Преобразование подводимой к насосу механической энергии в энергию движущейся жидкости в лопастных насосах производится за счет непосредственного силового воздействия лопастей рабочего колеса на жидкость, заполняющую его каналы. Рабочее колесо является основным элементом насоса, а кинематические показатели (значения и направление скоростей, траектория движения и т.п.) движущейся через колесо жидкости оказывают решающее влияние на энергетические параметры колеса (напор, подача, КПД).

Жидкость, проходя через колесо, совершает сложное движение: она входит в колесо в направлении, параллельном оси вала, а выходит перпендикулярно оси. При этом каждая частица жидкости вращается вместе с колесом с окружной скоростью υ и одновременно перемещается вдоль лопатки с относительной скоростью ω. Согласно общим положениям механики жидкости, абсолютная скорость υ в области лопастного колеса может быть получена как геометрическая сумма относительной ω и переносной u скоростей. В векторной форме: υ=ω+ū

Параллелограмм скоростей потока в рабочем колесе центробежного насоса.

В основу представления об установившемся движении потока через рабочее колесо центробежного насоса положена гипотеза о струйном течении жидкости. Согласно этой гипотезе траектория каждой частицы жидкости в пределах межлопастного канала колеса по форме совпадает с кривой очертания лопасти.

Предположим, что заданы геометрические размеры рабочего колеса центробежного насоса (рис. а), его объемная подача Q и частота вращения n. Определим, пользуясь гипотезой о струйном течении, значения и направления относительной скорости на плоском сечении колеса, перпендикулярном оси насоса в некоторой точке потока, отстоящей от оси вращения на расстоянии r (рис. б). Для определения значения относительной скорости воспользуемся уравнением неразрывности, составив его для цилиндрического сечения потока, проходящего через рассматриваемую точку. Площадь этого сечения обозначим через f_r. Радиальная составляющая скорости потока

ω_r=Q/ f_r

Учитывая коэффициентом ψ стеснение сечения телом лопастей шириной b, получим:

f_r=2πrbψ

ω_r=Q/2πrbψ

Переносная скорость в рассматриваемой точке потока равна окружности скорости вращения колеса

u= ω=(2πrn)/60

и направлена по касательной к окружности радиусом r в сторону вращения.

Радиальная составляющая относительной скорости ω_r перпендикулярна вектору переносной скорости u. Касательная к поверхности лопасти, по которой направлена относительная скорость ω образует угол β с направлением обратным переносной скорости. Проведя из конца вектора ω_r прямую, параллельную направлению скорости u, до пересечения с этой касательной, получим, согласно плану скоростей, в этой точке пересечения конец вектора относительной скорости ω. Значение относительной скорости:

ω= ω_r/sin β =Q/(2πrbψ sin β)

Суммируя по правилу параллелограмма относительную и переносную скорость, получим полную скорость. Поскольку радиальная составляющая ω_r относительной скорости равна радиальной составляющей υ_r абсолютной скорости, то значение скорости υ может быть определена из соотношения:

υ= υ_r/sinα=Q/(2πrbψsinα)

где α – угол между направлениями абсолютной и переносной скоростей.

Таким образом, гипотеза о струйном течении жидкости, основанная на предположении о бесконечном числе лопастей, позволяет построить параллелограмм скоростей в любой точке внутри рабочего колеса насоса.

Коэффициент стеснения ψ равен отношению действительной площади сечения потока к площади сечения свободного от лопастей:

ψ=(2πrb – zbs)/ 2πrb

где z – число лопастей, s – толщина лопастей в рассматриваемом цилиндрическом сечении.

Обозначая через t=2πr/z шаг, расстояние по окружности между одноименными точками смежных лопастей, получим, что коэффициент стеснения

ψ=(t – s)/t

Толщина лопасти s может быть выражена через нормальную толщину δ и угол β

S= δ/sin β

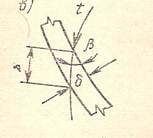
Величина окружной составляющей абсолютной скорости u жидкости характеризует закрутку жидкости на входе в рабочее колесо u₁ и на выходе u₂. На входе в рабочее колесо закрутка жидкости может отсутствовать u₁=0 или u₁≠0, при этом она направлена в сторону вращения (положительная) и против вращения (отрицательная). Закрутка потока применяется с целью улучшения антикавитационных свойств насоса. Закрутка в сторону вращения рабочего колеса способствует увеличению всасывания жидкости насосом, против вращения насоса – увеличение напора.

Построим треугольники скоростей на входе и выходе в рабочем колесе насоса.

При построении треугольников скоростей осевых насосов следует учитываьб две особенности:

1) Скорости переносного движения всех точек лопастей рабочего колеса в том числе входной и выходной кромок для рассматриваемого цилиндрического слоя, определяя по формуле: u=u₁= u₂=2πr_in/60

2) В силу сплошности потока осевые составляющие абсолютной скорости υ во всех точках рассматриваемого цилиндрического слоя должна быть:

υ_z= υ sinα = υ₁sinα₁ = υ₂sinα₂

υ_z=ω sinβ = ω₁sinβ₁ = ω₂sinβ₂

υ_z= ΔQ/2πr_iΔr_i = 4Q/π(D² – d²_вт)

где D – внешний диаметр рабочего колеса, d_вт – диаметр втулки.

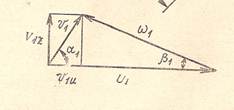
Таким образом, треугольники скоростей на входной и выходной кромках лопастей имеют одинаковое основание и равную высоту.

Принципиальное отличие работы решетки профилей от единичного профиля заключается в том, что направления скорости жидкости до и после решетки различны, т.к. решетка профилей меняет направление скорости на бесконечности, а единичный профиль этого направления не меняется.

«Основное уравнение насоса (уравнение Эйлера)»

Напор, развиваемый насосом, и коэффициент полезного действия тесно связан со значением и направлением скоростей потока жидкости в межлопастных каналах колеса. Для установления этой связи воспользуемся классической теоремой об изменении моментов количества движения, которая может быть сформирована следующим образом: производная по времени главного момента количества движения системы материальных точек относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту систему. Математически теорема записывается следующим образом:

d[(mυ)r] / dt = ΣM

где m – масса рассматриваемой системы материальных точек;

υ – абсолютная скорость их движения;

r – расстояние до оси.

Удобство теоремы об изменении моментов количества движения в приложении к сплошной среде заключается в том, что с ее помощью динамическое взаимодействие между жидкостью и обтекаемыми поверхностями можно определить по характеру течения в контрольных сечениях без учета структуры потока внутри выделенного объема.

При подаче насоса Q масса жидкости, участвующей в движении, составляет: m = ρQ, где ρ – плотность жидкости.

Момент количества движения на выходе из колеса:

M_к.д.2 = ρQυ₂r_вых

Момент количества движения жидкости на входе в колесо

M_к.д.1 = ρQυ₁r_х

С учетом сделанных допущений это уравнение может быть переписано в виде:

ΣM = M_к.д.2 - M_к.д.1 = ρQ(υ₂r_вых - υ₁r_вх)

Из треугольников скоростей следует, что

r_вх = D₁cos α₁ / 2

r_вых = D₂cos α₂ / 2

где D₁ – диаметр всаса, D₂ – диаметр рабочего колеса.

Нарисуем параллелограммы скоростей потока на входе в рабочее колесо центробежного насоса и на выходе из него.

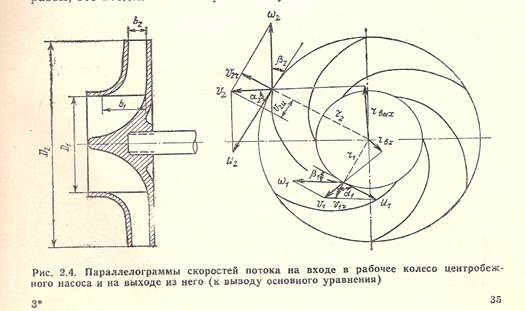
Подставляя значение r_вых и r_вх, получим:

ΣM = ρQ(υ₂r_вых*D₂/2 - υ1rвх*D₁/2)

Все внешние силы, действующие на массу жидкости, заполняющей межлопастные каналы рабочего колеса, можно разделить на три группы:

1) Сила тяжести.

2) Давление на жидкость.

3) Силы на обтекаемых поверхностях рабочего колеса.

Таким образом, момент всех внешних сил относительно оси вращения сводятся к моменту динамического воздействия рабочего колеса M_р.к. на протекающую через него жидкость, т.е.

ΣM = M_р.к.

При этом, мощность, передаваемая жидкости рабочим колесом насоса, равна произведению M_р.к. ω = ρgQH_т

где H_т – теоретический напор, создаваемый рабочим колесом насоса.

H_т = (u₂υ₂cos α₂ – u₁υ₁cos α₁) / g

Эта зависимость была впервые выведена в середине 18 века математиком и механиком Леонардом Эйлером, членом Петербургской академии. Она получила название уравнение Эйлера или основное уравнение лопастного насоса.

«Законы подобия применительно к центробежным насосам»

Геометрическое подобие в гидромеханике означает подобие всех поверхностей, ограничивающих и направляющих поток. При моделировании гидравлических машин два насоса могут быть названы подобными, если все линейные размеры одного из них (модель) в одинаковое число раз меньше или больше соответствующих размеров другого (натура). Математически гидравлическое подобие сравниваемых насосов определяется посредством линейного коэффициента подобия:

M_i – D_н / D_м = b_н / b_м = … = const

где D_н, b_н, и D_м, b_м – соответственно диаметры и высоты рабочих колес модельного и натурного насосов.

Геометрическое подобие означает также постоянство отношений любых других размеров у модели и натуры:

b_м / D_м = b_н / D_н = … = const

Кинетическое подобие означает, что безразмерные поля скоростей в рассматриваемых потоках должны быть одинаковы, т.е. отношения скоростей всех соответствующих частиц жидкости, участвующих в движении, должны быть равны между собой, а траектории движения в сравниваемых гидравлических системах – геометрически подобны.

Математически условия кинематического подобия могут быть выражены в виде ряда отношений

υ_н / υ_м = ω_н / ω_м = u_н / u_м = n_н D_н / n_н D_н = … = const

Динамическое подобие кроме соблюдения условий геометрического и кинематического подобия означает пропорциональность сил, действующих в соответствующих точках потока.

В практике моделирование гидравлических машин очень большое значение имеет критерий подобия Эйлера. Он может быть выражен следующим образом:

E_u = p / ρυ² = gH / υ²

Принимаемые в условии расход Q, напор Н и диаметр рабочего колеса D. Условие подобия может быть записано в виде:

Q_н / D²_н √Н_н = Q_м / D²_м √Н_м

Уравнение устанавливает зависимость между основными энергетическими параметрами (подача, напор) модельного и натурного насосов.

«Коэффициент быстроходности»

Одни и те же значения подачи и напора могут быть получены в насосах с различной частотой вращения.

Коэффициентом быстроходности n_s насоса называется частота вращения другого насоса таких же размеров, при которых, работая в том же режиме с полезной мощностью в 1л.с., он создает напор, равный 1м.

n_s = (n√N) / (H*Н^0,25)

Подставляя вместо мощности N ее значение ρgQH / 763 для насосов перекачивающих воду (ρ = 1000 кг/м³) получим другую формулу для определения коэффициента быстроходности (или частота вращения рабочего колеса):

n_s = 3,65 * (n√Q / H^0.75)

«Кавитация насосов. Высота всасывания центробежного насоса»

Кавитация представляет собой процесс нарушения сплошного потока жидкости, происходящий там, где местное давление, понижаясь, достигает некоторой критической величины. Процесс сопровождается образованием пузырьков, насыщенных паром жидкости, а также воздухом, выделяющемся из жидкости. Поэтому данный процесс отождествляется с кипением. При большом количестве в жидкости растворенного воздуха уменьшение давления приводит к выделению из нее воздуха и образованию газовых полостей (каверн), в которых давление выше, чем давление насыщенных паров жидкости.

Разрушение или «захлопывание» кавитационных пузырей при переносе их потоком в область с давление выше критического происходит очень быстро и сопровождается своего рода гидравлическими ударами. Наложение большого числа таких ударов приводит к появлению характерного шипящего звука, который всегда сопутствует кавитации. В подавляющем большинстве случаев кавитация сопровождается разрушением поверхности, но которой возникают кавитационные пузыри. Это разрушение является одним из самых опасных последствий кавитации, называется кавитационной энергией. Механические повреждения рабочих органов гидравлических машин в результате кавитационной эрозии за относительно короткий срок могут достигнуть размеров, затрудняющих их нормальную эксплуатацию и даже ее практически невозможной.

Высота всасывания насосов.

Рассмотрим три основные схемы установки центробежных насосов по отношению к уровню свободной поверхности жидкости в приемном резервуаре.

Схема 1. Уровень свободной поверхности расположен ниже оси рабочего колеса насоса.

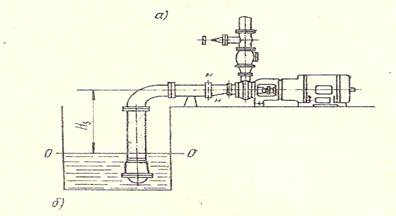
Давление на входе в насос определяется величиной:

H_s = (P_атм / ρg) – (P_н / ρg) – (υ²_н / 2g) – hω_o-н

где H_s – геометрическая высота всасывания (разность отметок оси рабочего колеса и свободной поверхности жидкости в резервуаре);

P_атм – атмосферное давление;

P_н – давление во всасывающем трубопроводе;

υ²_н – скорость движения жидкости во всасывающем трубопроводе;

ω_o-н – потери напора во всасывающей линии насоса, м (или сумма потерь на входе, потерь на трение по длине трубопровода, местные сопротивления).

Величина вакуума на входном сечении определяют по формуле:

H_в = [(P_атм - P_н) / ρg - υ²_н / 2g]

H_в – вакуумметрическая высота всасывания.

Зависимость между высотой всасывания и вакуумметрической определяется уравнением:

H_s = H_в - hω_o-н

или H_в = H_s + hω_o-н

Схема 2. Уровень свободной поверхности расположен выше оси рабочего колеса насоса.

H_s = hω_o-н - H_в

H_в = hω_o-н - H_s

Величина значения H_s будет отрицательной. Отрицательное значение геометрической высоты всасывания называется подпором.

Схема 3. Откачка жидкости из замкнутого резервуара. Принципиальное отличие данной схемы работы насоса от рассматриваемой ранее схемы 2 заключается в вакуумметрической высоте всасывания.

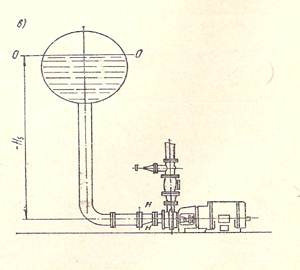
H_в = (P_атм + Р_изб + Р_н) / ρg - υ²_н / 2g

Р_изб – избыточное давление. Оно может быть положительным, отрицательным и зависит от технологического назначения насоса и конструктивных особенностей.

«Характеристики центробежных насосов»

Основными параметрами лопастных насосов являются: напор Н, подача Q, мощность N, частота вращения n и коэффициент полезного действия η. Основной характеристической кривой насоса является график, выраженный зависимостью развиваемого напора от подачи Н = f(Q) при постоянной частоте вращения n=const.

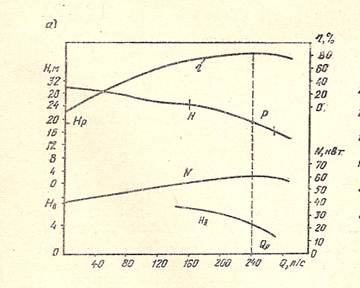
Кривые Q-H, Q-N, Q-η, Q-H_в называются характеристиками центробежного насоса и имеются в каталогах, справочниках и в паспортах на насосы.

Дата добавления: 2014-01-20