Новочеркасск 2012

Лекции

Примеры редактирования звука

Нарезка дорожек стереозаписи

· Откроем MP3 файл.

· Выделим часть, которая станет первым музыкальным фрагментом, и прослушаем его, используя кнопку Воспроизвести.

· Пока часть выделена, выберем команду Экспортировать выделенное.

· Перейдем к следующему фрагменту.

Наложение голоса на фоновую музыку

Audacity позволяет легко записывать и микшировать фонограммы.

Подготовим файлы для микширования:

· запись, сделанную с микрофона;

· аудиодорожки фонограммы.

Выберите из меню Проект / Импорт звукового файла (голоса и фонограмм).

Прослушайте ваш проект. Используйте для сдвига дорожек во времени.

Если какая-то дорожка слишком громкая относительно другой, используйте команду Усилить.

В конце экспортируйте ваш проект в какой-то распространенный формат.

Человек-оркестр

Вы можете петь сам с собой!

· Откройте настройки из меню файл. Откройте закладку I/O tab и отметьте " Воспроизводить существующие дорожки при записи новой ". Сохраните изменения.

· Щелкнете Click the Record button. Напойте что-либо.

· Щелкните кнопку записи еще раз. Audacity начнет записывать все дорожки сразу.

· После записи дорожек для синхронизации используйте инструмент

Параллельная запись на разные дорожки

Как записать два источника звука на разные дорожки? Например, если вы пишете 2-х актеров? Каждый должен записываться на свою дорожку.

Проведем настройки.

Откройте Настройки и выберите закладку Audio I/O.

Убедитесь, что установлены параметры, как показаны на рисунке: Стерео, "Воспроизводить существующие дорожки при записи новой", "Аппаратное сквозное воспроизведение ".

Подсоедините 2 источника к 2-м стереовходам звуковой платы.

Установите разделить стереодорожку на 2 моно:

Каждую дорожку замените на моно:

Проведите запись.

«ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ,

ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧАХ»

(Часть VIII: оценка погрешностей)

Оглавление

§1. Учет погрешностей вычислений. 3

§2. Оценка погрешностей результатов действий над приближенными значениями чисел. (Строгий учет погрешности) 5

§3. Приближенные вычисления без учета погрешностей. 6

§4. Связь между числом количества верных цифр. 7

и относительной погрешностью. 7

§5. Прямая задача теории погрешностей. 9

(функции от приближенных значений аргументов). 9

§6. Обратная задача теории погрешностей. 11

§7. Метод границ. 13

§8. Математические модели и численные методы. 15

§9. Понятие корректно поставленной. 16

и некорректно поставленной задач. 16

§10. Вспомогательные сведения из функционального анализа. 17

§11. Решение уравнений с одним неизвестным. Дихотомия. 19

§12. Метод простой итерации для решения алгебраических и трансцендентных уравнений. 20

§13. Метод Ньютона. Решение уравнений с одной переменной. 22

§14. Метод хорд. Метод секущих. 25

§15. Метод Гаусса решения систем уравнений. 27

§16. Метод квадратного корня. 28

ЛИТЕРАТУРА.. 30

§1. Учет погрешностей вычислений.

При решении математических задач могут возникнуть погрешности по различным причинам:

1. При составлении математической модели физического процесса или явления приходится принимать условия, упрощающие постановку задачи. Поэтому математическая модель не отражает реальный процесс, а дает его идеализированную картину. Погрешность, возникающая при этом, называется погрешностью постановки задачи.

2. Часто приходится для решения задачи применять приближенный метод (интеграл заменяют квадратурной суммой, производную заменяют разностью, функцию – многочленом). Погрешность, возникающая при этом, называется погрешностью метода.

3. Часто исходные данные заданы не точно, а приближенно. При выполнении вычислений погрешность исходных данных в некоторой степени переходит в погрешность результата. Такая погрешность называется погрешностью действий.

4. Погрешность, возникающая при округлении бесконечных и конечных десятичных чисел, имеющих большее число десятичных знаков, чем надо в округлении, называется погрешностью округления.

Определение. Пусть х – некоторое число, число а называется его приближенным значением, если а в определенном смысле мало отличается от х и заменяет х в вычислениях, .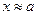

Определение. Погрешностью приближенного значения а числа х называется разность , а модуль этой погрешностью называется абсолютной погрешностью.

Если , то а взято с недостатком.

Если , то а взято с избытком.

Определение. Границей погрешности приближенного значения а числа х называется всякое неотрицательное число , которое не меньше модуля погрешности: .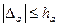

Говорят, что приближение а приближает число х с точностью до , если , , .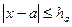

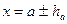Пример. Пусть а=0,273 – приближенное значение х с точность до 0,001. Указать границы, в которых заключается х.

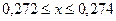
При округлении чисел считают, что границы погрешности округления равна половине единицы округляемого разряда:

, α – порядок округления разряда.

Определение. Относительной погрешностью приближенного значения а числа х называется отношение

.

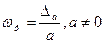Пример. Округлить до десятых число 27,52 и найти погрешность и относительную погрешность округления:

,

,

.

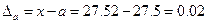Также как и абсолютная погрешность относительная погрешность не всегда может быть вычислена и приходится оценивать ее модуль. Модуль относительной погрешности выражается в процентах. Чем меньше модуль относительной погрешности, тем выше качество приближения.

Определение. Границей относительной погрешности приближенного значения а числа х называется всякое неотрицательное число , которое не меньше модуля относительной погрешности: .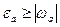

Установим связь между границами погрешностей абсолютной и относительной:

- граница относительной погрешности;

- граница абсолютной погрешности.

.

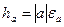§2. Оценка погрешностей результатов действий над приближенными значениями чисел. (Строгий учет погрешности)

Пусть 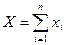, где – число с заданными своими приближениями с точностью до : .

Обозначим через .

, где 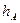- граница погрешности суммы приближенного значения .

Утверждение 1. Сумма границ погрешностей приближенных слагаемых является границей погрешности их алгебраической суммы.

Доказательство: .

ЧТД.

Утверждение 2. Среди границ относительной погрешности суммы приближенных слагаемых существует такая, которая не превосходит наибольшей из границ относительной погрешности слагаемых:

.

Утверждение 3. Сумма границ относительных погрешностей сомножителей является границей относительной погрешности их произведения:

.

Следствие 1. При умножении приближенных значений числа на точный множитель к, граница относительной погрешности не меняется, а граница абсолютной погрешности увеличивается в 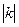раз.

Следствие 2. Произведение границы относительной погрешности приближенного значения а числа х на является границей относительной погрешности результата возведения числа а в целую положительную степень n:

.

Следствие 3. Частное границы относительной погрешности приближенного значения а числа х и n является границей относительной погрешности корня n-й степени из а:

.

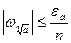Следствие 4. Сумма границ относительных погрешностей приближенных значений делимого и делителя является границей относительной погрешности частного.

§3. Приближенные вычисления без учета погрешностей.

Правило 1. Для того, чтобы вычислить алгебраическую сумму приближенных слагаемых нужно:

1. среди слагаемых выбрать наименее точное (имеет наименьшее число разрядов после запятой);

2. все остальные слагаемые округлить, сохраняя один запасной разряд, следующий за последним разрядом выделенного слагаемого;

3. сложить полученные после округления числа;

4. округлить полученный результат до предпоследнего разряда.

Пример. S=2.737+0.77974+27.1+0.2832.74+0.78+27.1+0.2830.9030.9.

Определение 1. Значащими цифрами в десятичной записи числа называется все его цифры кроме нулей, записанных слева от первой цифры не равной 0.

0,00237 – 3 значащие цифры;

0,02000 – 4 значащие цифры.

Правило 2. Для того, чтобы вычислить произведение (деление) приближенных чисел нужно:

1. выделить сомножитель, содержащий наименьшее число значащих цифр;

2. округлить остальные сомножители, оставляя на одну значащую цифру больше, чем в выделенном сомножителе;

3. произвести умножение (деление);

4. округлить полученный результат, сохраняя столько значащих цифр, сколько их в выделенном сомножителе.

Пример. Р=3,34*0,7*4,748=4,7*3,3*0,710,6571*.

Правило 3. При возведении приближенного значения в квадрат или куб, при извлечении квадратного или кубического корня, в результате следует оставлять столько значащих цифр, сколько их имеет основание.

Правило 4. Если число является результатом промежуточных действий, то следует сохранить в нем на 1-2 цифры больше, чем указано в правилах 1-3.

§4. Связь между числом количества верных цифр

и относительной погрешностью.

Пусть .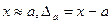

Определение. Цифра приближенного значения а называется верной, если модуль его погрешности не превосходит половины единицы этого разряда.

.

Очевидно, что все цифры, стоящие слева от верной цифры – верные.

Пример. Пусть х=27,421, а=27,381, .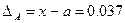

Выясним, какие цифры верные в приближении а?

4 – 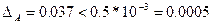, следовательно, 4 – неверная;

8 – 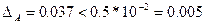, следовательно, 8 – неверная;

3 – , следовательно, 3 – верная.

3,2,7 – верные цифры.

Пусть известно количество n верных значащих цифр в приближении а, тогда а запишем:

.

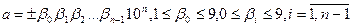Так как цифра, стоящая в разряде -(n-1) верна, то погрешность

,

тогда .

В качестве границы относительной погрешности можно взять .

Итак, доказана теорема 1.

Теорема 1. Если приближение имеет n верных значащих цифр, то число является границей его относительной погрешности.

Теорема устанавливает связь между числами верных значений и его относительной погрешностью.

Замечание. Пусть приближение имеет n верных значащих цифр и – его первая значащая цифра, тогда число 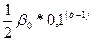является границей относительной погрешности.

Пример. .

Итак, граница относительной погрешности приближенного значения зависит от первой значащей цифры , количества верных цифр приближения, но не зависит от порядка приближения.

Теорема 2. Если граница относительной погрешности приближения равна , то приближение имеет не менее n значащих цифр.

Доказательство. Пусть - первая значащая цифра приближения а и n – порядок, тогда .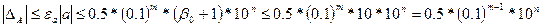

Из определения следует, что –(m-1) – цифра, записанная в этом разряде верная, цифры, записанные левее тоже верные, то есть m верных цифр.

ЧТД.

Пример. Если известно, что относительная погрешность приближения 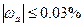, то согласно теореме 2, это приближение имеет ровно 3 верные значащие цифры.

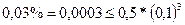, следовательно, по теореме 2, приближение имеет не менее 3-х верных значащих цифр.

§5. Прямая задача теории погрешностей

(функции от приближенных значений аргументов).

Пусть функция 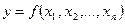определена и непрерывно-дифференцируема по всем переменным в области .

Переменные заданы своими приближениями:

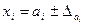и точка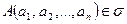

Известна погрешность элементов 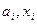. Необходимо оценить погрешность .

.

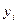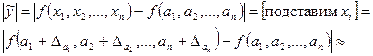Предположим, что 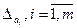малы, поэтому их произведениями, квадратами и более высокими степенями можно пренебречь.

Если , то последнюю часть можно поделить на функцию

.

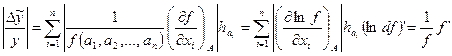
Пример. Вычислить величину погрешности приближенного значения большего корня уравнения.

В приближенной записи используют только верные цифры, обусловленные погрешностью приближенных значений коэффициентов.

,

.

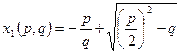
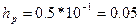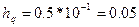Теперь обозначим .

Рассмотрим

.

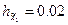§6. Обратная задача теории погрешностей.

Все задачи теории погрешностей делятся на прямые и обратные.

Прямая задача: определить погрешность данной функции от приближенных значений аргументов, заданных с известной относительной погрешностью или с заданной точностью.

Обратная задача: какими должны быть относительная и абсолютная погрешности, чтобы модуль относительной или абсолютной погрешности заданной функции не превышал заданной величины.

Дата добавления: 2014-01-20