Вероятностный подход к измерению информации

СОДЕРЖАТЕЛЬНЫЙ ПОДХОД ПРИ ИЗМЕРЕНИИ ИНФОРМАЦИИ

Как отмечалось выше, если после получения какого-то сообщения неопределенность знаний уменьшается в два раза, то это сообщение несет в себе 1 бит информации. Т.е., если событие имеет два исхода, то при наступлении каждого из них неопределенность знаний уменьшается в два раза. Количество информации в сообщении о том, что наступило одно из этих событий, равно 1 биту.

Таким образом, количество информации, полученное из сообщения о том, что наступило одно из N равновозможных событий, можно вычислить по формуле:

х = log₂N,

где х – количество информации в сообщении (в битах), N – количество равновозможных (равновероятных) событий, только одно из которых наступило.

Задача 1. Бросают игральный кубик. Найти количество информации в сообщении о том, что выпало число 5.

N = 6, х = log₂N = log₂6» 2,58 бит

Задача 2. В корзине лежат 8 шаров, все разного цвета. Найти количество информации в сообщении о том, что наугад вынули красный шар.

N = 8, х = log₂N = log₂8 = 3 бита

Задача 3. При угадывании целого числа в диапазоне от 1 до N было получено 1 байт информации. Найти N.

х = log₂N, отсюда N = 2^x

x = 1 байт = 8 бит

N = 2⁸ = 256

Пусть в результате испытания наступило некоторое событие. Вероятность его наступления можно вычислить по формуле:

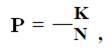
где N – количество всех возможных исходов испытания, K – количество исходов испытания, удовлетворяющих данному событию.

Количество информации в сообщении о том, что наступило одно из возможных событий можно вычислить по формуле:

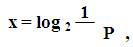
где P – вероятность наступления события, х – количество информации в сообщении о том, что наступило данное событие.

Задача 1. В корзине лежат 16 шаров: 4 синих и 12 красных. Найти количество информации в сообщении о том, что из корзины наугад вынули синий шар.

N = 16

K = 4

P = K/N = 4/16 = 1/4

x = log₂(1/P) = log₂4 = 2 (бита)

Задача 2. В классе 32 ученика. Учитель вызывает одного из них к доске. Количество информации в сообщении «Вызвали девочку» равно двум битам. Найти количество мальчиков и девочек и количество информации в сообщении о том, что к доске вызвали мальчика.

N = 32

Пусть K_д – количество девочек, тогда (32-K_д) – количество мальчиков.

x = log₂(1 / P), отсюда P = 1 / 2^х

x_д = 2 бита

Р_д = 1 / 2² = 1/4

С другой стороны:

Р_д = K_д / N = K_д / 32

Р_м = (32-K_д)/ N = (32-K_д) / 32 = 1- K_д / 32

1/4 = K_д / 32

K_д = 8, К_м = 32-8 = 24

Р_м = 1-8/32 = 3/4

х_м = log₂(1 / P) = log₂(4/3)» 3,58

Итак, в классе 8 девочек и 24 мальчика, количество информации в сообщении о том, что вызвали мальчика равна 3,58 бит.

Задача 3. В ящике лежат красные, синие и желтые шары. Наугад вынули один шар. Информационный объем сообщения «Вынули красный шар» равен трем битам. Количество информации в сообщении «Вынули синий шар» равно двум битам. Известно, что в ящике 5 желтых шаров. Найти количество всех шаров.

Пусть K_кр – количество красных, K_с – количество синих, K_ж – количество желтых шаров, N – общее количество шаров.

x_кр = 3 бита

x_с = 2 бита

K_ж = 5

P = 1 / 2^х

P_кр = 1 / 2³ = 1/8

P_с = 1 / 2² = 1/4

P_ж = K_ж / N = 5/N

Так как вынуть из ящика можно либо красный, либо синий, либо желтый шар, то P_кр + P_с + P_ж =1.

1/8+1/4+5/N = 1

3/8 + 5/N = 1

5/N = 1-3/8

5/N = 5/8

N = 8

Итак, в ящике 8 шаров.

Дата добавления: 2014-01-20