
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Цилиндрические винтовые пружины сжатия - растяжения
|
|
|
|
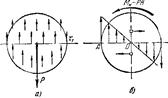
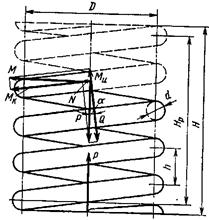 Под действием сил Р сжатия или растяжения в любом сечении прутка, из которого она навита, возникают напряжения сдвига и кручения. Если пренебречь углом подъёма винтовой линии прутка, который реально колеблется в пределах 5-120, то напряжение сдвига
Под действием сил Р сжатия или растяжения в любом сечении прутка, из которого она навита, возникают напряжения сдвига и кручения. Если пренебречь углом подъёма винтовой линии прутка, который реально колеблется в пределах 5-120, то напряжение сдвига 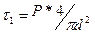 ,
,
а напряжение кручения
 .
.
Суммарное напряжение
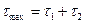 =
= 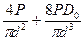 . Обычно первым слагаемым пренебрегают в виду его относительной малости и с учётом того, что максимальные напряжения (см. эпюры) возникают в периферийных слоях сечения прутка.
. Обычно первым слагаемым пренебрегают в виду его относительной малости и с учётом того, что максимальные напряжения (см. эпюры) возникают в периферийных слоях сечения прутка.
Эти же результаты можно получить разложив общий момент М, возникающий при сжатии- растяжении пружины на крутящий Мк =Р*0,5D0*Cosa и изгибающий Ми = Р*0,5D0*Sina.
Отсюда, вводя поправку на угол подъёма витка через коэффициент k и пренебрегая составляющей от Ми, получим значение максимального напряжения в периферийных слоях сечения прутка 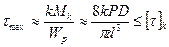 . Обычно принимают [τ]к = 0,5σв и при пульсирующей нагрузке понижают это значение в 1,25 – 1,5 раза.
. Обычно принимают [τ]к = 0,5σв и при пульсирующей нагрузке понижают это значение в 1,25 – 1,5 раза.
Коэффициент k вычисляется по формуле 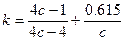 , где величина
, где величина 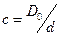 называется индекс пружины, D0 – средний диаметр пружины.
называется индекс пружины, D0 – средний диаметр пружины.
Значение коэффициента k в зависимости от индекса пружины с можно принять из таблицы
| с | ||||||
| k | 1,37 | 1,29 | 1,24 | 1,17 | 1,14 | 1,11 |
Из приведенных выражений, заменяя 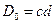 , получим формулу для определения диаметра проволоки (прутка) при проектном расчёте пружин
, получим формулу для определения диаметра проволоки (прутка) при проектном расчёте пружин 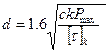 .
.
Работа А статических сил Р при линейном перемещении пружины (сжатии или растяжении)- λ определяется из выражения 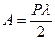 . Потенциальная энергия U, накапливаемая от воздействия сил, Р как правило, определяется с учётом только крутящих моментов. Влияние поперечных сил в сечении прутка не учитывается. Из курса сопротивления материалов потенциальная энергия при закручивании прутка
. Потенциальная энергия U, накапливаемая от воздействия сил, Р как правило, определяется с учётом только крутящих моментов. Влияние поперечных сил в сечении прутка не учитывается. Из курса сопротивления материалов потенциальная энергия при закручивании прутка 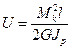 , где
, где 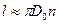 - длина развернутой пружины,
- длина развернутой пружины,
n – число витков пружины, 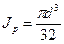 - полярный момент инерции сечения круглого прутка,
- полярный момент инерции сечения круглого прутка,
G – модуль сдвига материала прутка. Подставляя значения Jp и l, п олучим 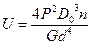 .
.
Приравняем потенциальную энергию пружины работе сил её деформации
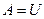 ;
; 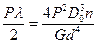 . Отсюда полное перемещения пружины от действия сил Р
. Отсюда полное перемещения пружины от действия сил Р
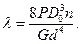 (Перемещение вычисляется только в пределах действия закона Гука).
(Перемещение вычисляется только в пределах действия закона Гука).
Величина усилия Р, при которой деформация (перемещение) пружины равно единице (1мм, 1см,..) называется жёсткостью пружины и обозначается 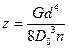 .
.
Жёсткость одного витка 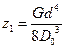 . Этот параметр введен в ГОСТ13776 и по нему выбираются стандартные пружины.
. Этот параметр введен в ГОСТ13776 и по нему выбираются стандартные пружины.
Число рабочих витков пружины 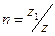 , полное число витков пружины
, полное число витков пружины 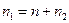 , где
, где
n2 –число опорных витков, которое принимается 1-1,5.
 С учётом принятого выражения для жёсткости пружины, её деформация при нагружении максимальной силой Р3,
С учётом принятого выражения для жёсткости пружины, её деформация при нагружении максимальной силой Р3, 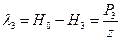 , соответственно предварительная деформация пружины
, соответственно предварительная деформация пружины 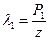 , рабочая деформация
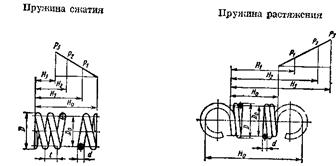
, рабочая деформация 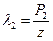 . Высота пружины сжатия при максимальной деформации
. Высота пружины сжатия при максимальной деформации
Н3 = (n1 – 0,5)d, а для пружины растяжения
Н0 = (Н0 +λmax)+ 2 hпр. Высота пружины сжатия в свободном состоянии H0 = H3 + λmax, а для пружины растяжения Н0 = nd +2 hпр, где hпр – высота зацепа в зависимости от его формы, равная (0,5-1)D. Длина развёрнутой пружины (без учёта длины зацепов)  .
.
Шаг пружины сжатия в ненагруженном состоянии 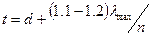 .
.
Шаг пружины растяжения 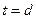 .
.
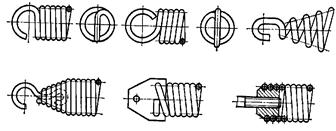 Рекомендуемая конструкция зацепов показана на рисунке
Рекомендуемая конструкция зацепов показана на рисунке
Приведенные выше расчётные зависимости справедливы для пружин, навитых из круглого прутка. Методика расчёта для пружин из прямоугольных прутков не меняется, но необходимо ввести коррекцию на геометрию прутка.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 610; Нарушение авторских прав?; Мы поможем в написании вашей работы!